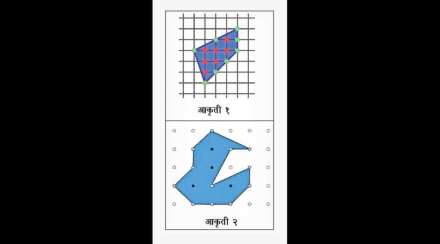
अनियमित बहुभुजाकृतीचे क्षेत्रफळ काढण्यासाठी एक सोपे सूत्र पिकचे प्रमेय देते. हे प्रमेय सर्वप्रथम १८९९ साली जॉर्ज अलेक्झांडर पिक (१८५९-१९४२) यांनी सिद्ध केले. ‘एखादे प्रतल, चौरस जालकाने (स्क्वेअर लॅटिस) झाकले असेल तर ज्या बहुभुजाकृतीचे सर्व शिरोबिंदू जालकातील चौरसांच्या छेदनबिंदूंवर म्हणजेच जालकबिंदूंवर (लॅटिस पॉइंट्स) येतात अशा बहुभुजाकृतीचे क्षेत्रफळ [अ+(ब/२)-१] चौरस एकक असते’ असे हे प्रमेय सांगते. या सूत्रात ‘अ’ = बहुभुजाकृतीच्या आतील जालकबिंदूंची संख्या आणि ‘ब’ = बहुभुजाकृतीच्या भुजांवरील जालकबिंदूंची संख्या. ब विषम असल्यास क्षेत्रफळ अपूर्णाकात व सम असल्यास पूर्णाकात येईल. थेट गुणाकाराचे कोणतेही पद नसणारे हे सूत्र वापरासाठी अतिशय सोयीचे आहे. आकृती १ मध्ये अ = ७, ब = ८ म्हणून क्षेत्रफळ १० चौरस एकक येते.
प्रथमदर्शनी शिरोबिंदू जालकबिंदूंवर असण्याची अट वाचून हे प्रमेय फार थोडय़ा विशिष्ट बहुभुजाकृतींकरताच उपयोगी आहे असे वाटते, पण चौरस जालकातील चौरसांच्या बाजूंची लांबी कमी करून दिलेल्या बहुभुजाकृतीच्या शिरोबिंदूंच्या निकट जालकबिंदू येतील अशी रचना केल्यास कुठल्याही बहुभुजाकृतीचे अंदाजे क्षेत्रफळ काढण्यासाठी हे प्रमेय वापरता येते, उदा. आकृती २.
या प्रमेयाच्या अनेक सिद्धतांपैकी काही सिद्धता विगमन (इंडक्शन) पद्धतीच्या आहेत. प्रतल आलेखाचे ऑयलरचे सूत्र वापरून दिलेली सिद्धता मार्टिन ऐग्नेर व गुंटर झिएग्लेर या लेखकांच्या ‘प्रूफ्स फ्रॉम ‘दि बुक’ ’ या गणितातील सुंदर सिद्धतांचे संकलन करणाऱ्या पुस्तकात समाविष्ट केली आहे. सर्वात महत्त्वाच्या १०० प्रमेयांच्या यादीत पिकच्या प्रमेयाचा समावेश आहे कारण ते पारंपरिक आणि आधुनिक अंकीय भूमितींना जोडते.
पिकच्या प्रमेयातील बहुभुजाकृती छिद्रविरहित असावी लागते पण बहुभुजाकृतीच्या अंतर्भागात जर एकंदर ‘छ’ छिद्रे असतील, तर त्या बहुभुजाकृतीचे क्षेत्रफळ [अ+ब/२+छ-१] चौरस एकक असेल असे या प्रमेयाचे व्यापक रूप सांगते. प्रतलीय बहुभुजाकृतीच्या सूत्राप्रमाणे फक्त पृष्ठे व अंतर्भागातील जालकबिंदूच्या संख्या वापरून त्रिमितीय बहुपृष्ठाकारांचे सूत्र मात्र मिळू शकत नाही, त्याची सिद्धता जॉन रीव्ह यांनी १९५७ साली दिली. अर्थात जालकबिंदूंची संख्या व इतर अधिक माहिती वापरून थोडे गुंतागुंतीचे उच्चमितीतील पिकचे सूत्र मिळवता येते. अलीकडच्या काळात फ्रीक वाएक (Wiedijk) यांनी पिकचे प्रमेय हे सिद्धता सहायक (प्रूफ असिस्टंट) म्हणजे गणिती प्रमेयांच्या सिद्धता संगणक व मानव यांनी एकत्रित शोधण्यासाठी वापरल्या जाणाऱ्या आज्ञावल्यांचे कौशल्य अजमावण्याची कसोटी म्हणून वापरले. पिकच्या प्रमेयाची लक्षणीय उपयोजने बीजगणित, विश्लेषण, संगणकशास्त्र अशा अनेक शाखांमध्ये आढळतात.
– प्रा. माणिक टेंबे
मराठी विज्ञान परिषद, वि. ना. पुरव मार्ग, चुनाभट्टी, मुंबई २२ office@mavipamumbai.org