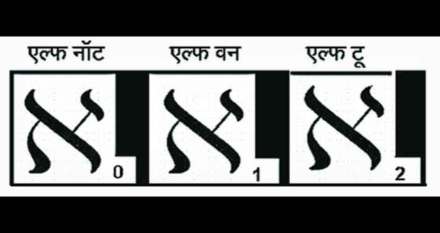
कॅण्टर यांनी सिद्ध केलेल्या संततकाच्या प्रमेयामुळे अपरिमेय संख्यांचा संच गणनीय नाही व त्याचा संचांक (एल्फ नॉट) हून मोठा आहे हे सिद्ध झाले. पण त्याचा संचांक c इतकाच आहे, याची सिद्धता मात्र कॅण्टर यांनी नाही, तर एर्नस्ट श्रॉडर (१८९६) आणि फेलिक्स बर्नस्टाइन (१८९८) या दोन गणितज्ञांनी स्वतंत्रपणे दिली. c हून मोठा संचांक शोधण्यासाठी कॅण्टर यांचे प्रयत्न सुरूच होते. अखेरीस १८९१ मध्ये कॅण्टर यांनी अतिशय महत्त्वाचे आणि नितांत सुंदर असे प्रमेय सिद्ध केले. ते कॅण्टरचे प्रमेय म्हणून ओळखले जाते. या प्रमेयात त्यांनी ‘स हा कुठचाही एक संच आणि प(स) हा स चा घातसंच (पॉवर सेट) असल्यास, स चा संचांक हा प(स) च्या संचांकाहून लहान असतो’, असे सिद्ध केले. प(स) म्हणजे स च्या सर्व उपसंचांचा संच. उदाहरणार्थ स = १,२ असल्यास प(स) = , १, २, १,२ होईल (इथे हा रिक्त संच आहे). प्रमेयाचे हे विधान सान्त (फायनाईट) तसेच अनंत सर्वच संचांना लागू पडते, त्यामुळे नैसर्गिक संख्यासंचास ‘न’ मानल्यास न चा संचांक हा प(न) च्या संचांकाहून लहान असणार. प(न)चा संचांक हा पप(न) या संचाच्या संचांकाहून लहान असणार. अशाप्रकारे न, प (न), पप(न),.. अशा एकाहून एक मोठय़ा संचाच्या संचांकांच्या संचांची अनंत क्रमिकाच गवसली. कॅण्टर यांनी प(न) च्या संचाकास (एल्फ वन), पप(न) च्या संचांकास स्2(एल्फ टू),.. अशी नावे दिली. एकाहून एक मोठे असे अनंत अनंत जन्माला घालणारे हे प्रमेय आणि त्याची सिद्धता मुळातूनच वाचून आनंद लुटावा अशी आहे. हजारो वर्षे ज्या अनंताची व्याख्याही गवसत नव्हती ती अनंताची कहाणी अनेक आश्चर्यकारक वळणे घेत एकाहून एक मोठय़ा अनंत अनंताचा शोध लागण्यापर्यंत येऊन पोहोचली. गणितज्ञ डेव्हिड हिलबर्ट यांनी कॅण्टर यांच्या या अनंताच्या सिद्धांतांना कॅण्टर यांनी निर्मिलेले अनंताचे नंदनवन असे म्हटले आहे आणि ते अगदी सार्थ आहे. अनंताच्या सिद्धांतातला एक राहून गेलेला दुवा म्हणजे हून मोठा आणि c हून लहान असा एखादा संचांक आहे का, याचे उत्तर मात्र कॅण्टर शोधत राहिले. तसा संचांक नसावा असा त्यांचा कयास होता. या विधानाला संततकाचे गृहीतक (कंटीन्युअम हायपोथिसिस) असे म्हटले जाते. त्याची सिद्धता मिळण्यापूर्वीच कॅण्टर यांचा मृत्यू झाला. पण त्या प्रयत्नाने पुढे गणिताच्या पायाबाबत एक वेगळेच वळण घेतले. - प्रा. माणिक टेंबे मराठी विज्ञान परिषद, वि. ना. पुरव मार्ग, चुनाभट्टी, मुंबई २२ office@mavipamumbai.org
