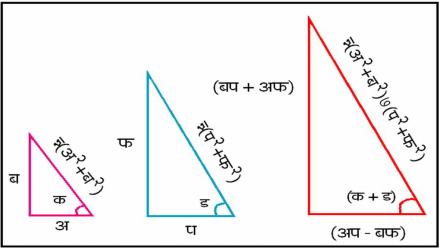
गुणाकार हा संख्यांचा असतो; मग काटकोन त्रिकोणांचा गुणाकार हे काय आहे? आपण याची फोड उदाहरण घेऊन करू. लेखासह दिलेल्या आकृतीमध्ये दाखवल्याप्रमाणे, समजा पहिल्या काटकोन त्रिकोणाचा पाया अ, उंची ब, पाया आणि कर्ण यांतील कोन क आहे; दुसऱ्या काटकोन त्रिकोणाचा पाया प, उंची फ, पाया आणि कर्ण यांतील कोन ड आहे. तर पायथागोरसच्या प्रमेयानुसार त्यांचे कर्ण क्रमश: न्न्(अ२+ब२) आणि न्न्(प२+फ२) असे असतील. या दोन त्रिकोणांचा गुणाकार ही संकल्पना सांगते की, उत्तर म्हणून मिळणारा आणखी एक काटकोन त्रिकोण असेल, ज्याचा कर्ण न्न्(अ२+ब२)७(प२+फ२), तर पाया (अप – बफ) आणि उंची (बप + अफ) असतील. तसेच त्याचा पाया आणि कर्ण यांतील कोन
(क + ड) असेल. जसे की, अ = ३, ब = २ आणि प = २, फ = १ असतील तर नवीन काटकोन त्रिकोणाचा पाया ४ आणि उंची ७ असतील आणि कर्ण न्न्६५ असेल.
हे कसे शक्य होते? यासाठी डायफॅण्टस याने इ.स. २०० मध्ये दिलेले पुढील सूत्र उपयोगी पडते : अ, ब, प आणि फ या धन वास्तव संख्यांसाठी (अ२+ब२) ७ (प२+फ२) = (अप – बफ)२ + (बप+अफ)२. या सूत्राची डावी बाजू पायथागोरसच्या प्रमेयानुसार रचल्यामुळे हे घडते. भूमिती आणि बीजगणित यांचा हा मिलाफ सहसा दुर्लक्षित राहतो.
आणखी एक उल्लेखनीय बाब म्हणजे, हे सूत्र दोन संमिश्र (कॉम्प्लेक्स) संख्यांच्या गुणाकाराशीही जोडलेले आहे. कारण
(अ+ब ्र) ७ (क+ख ्र) = (अक-बख) + (अख+बक), इथे ्र = न्न्-१ ही काल्पनिक संख्या आहे. एका अर्थाने काटकोन त्रिकोणांचा गुणाकार हा संमिश्र संख्यांना सदिश (व्हेक्टर) स्वरूपात दर्शवतो. म्हणजे डायफॅण्टसच्या सूत्राचा उपयोग त्याच्यानंतर सुमारे १६०० वर्षांनी संमिश्र संख्यांच्या गुणाकाराच्या निर्मितीत झाला, हे अचंबित करते.
पण गणित, विशेषत: शुद्ध गणित हे सहसा काळाच्या पुढे राहत आलेले आहे. उदाहरणार्थ, शुद्ध गणिताचे पाईक सुप्रसिद्ध गणितज्ञ जी. एच. हार्डी व श्रीनिवास रामानुजन यांचे कार्य. त्यांचे अतिशय अमूर्त गणिती निष्कर्ष सध्याच्या अंकीय तंत्रज्ञान विकसनात कळीची भूमिका बजावत आहेत, ज्याची त्यांनी कधीही अपेक्षा केली नव्हती!
– डॉ. विवेक पाटकर
मराठी विज्ञान परिषद
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org