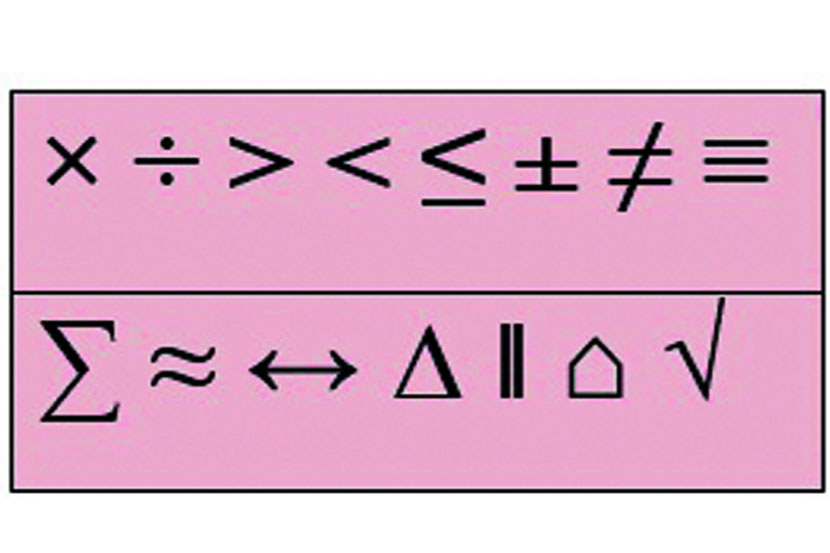गणिताची समग्र व्याख्या करणे खूप कठीण आहे. कुणाला ते विज्ञान वाटते, तर कुणाला कला. पण वास्तव जगातील समस्यांना समूर्ताकडून अमूर्त गणिती प्रारूपात रूपांतरित करणारी गणित ही एक सामर्थ्यवान भाषा नक्कीच आहे.
या भाषेचे महत्त्वाचे वैशिष्टय़ म्हणजे तर्ककठोर शिस्त आणि नेमकेपणा. प्रत्येक नियमाला अपवाद असतो असे म्हणतात; पण गणित कणभरही अपवाद वा संदिग्धता मान्य करत नाही. गणितात कुठचेही विधान वापरताना ते आधी सिद्ध करावे लागते आणि सिद्ध करताना किमान गृहीतके व पूर्वसिद्ध विधानेच वापरता येतात. काटेकोरपणा इतका की, अनंत वास्तव संख्यांपैकी फक्त शून्याला गुणाकारव्यस्त (मल्टिप्लिकेटिव्ह इन्व्हर्स) नाही. तरीही ‘वास्तव संख्यांना गुणाकारव्यस्त असतो’ असे विधान केले जात नाही. ‘शून्येतर वास्तव संख्यांना गुणाकारव्यस्त असतो’ असेच विधान गणितज्ञ करतील. अशी शिस्त उभारणे हे गणितज्ञांसाठीही एक आव्हानच असते. त्यासाठी अनेकदा गणितज्ञांच्या कित्येक पिढय़ांना प्रयास करावे लागतात. उदाहरणार्थ, कलनशास्त्रातील सीमा (लिमिट), विकलन (डिफरन्शिअल कॅलक्युलस) तसेच संकलन (इंटिग्रल कॅलक्युलस) या संकल्पना मांडून १७ व्या शतकात न्यूटन आणि लायब्निझ यांनी कलनशास्त्राचा पाया रचला. पण त्यांच्या वर्णनात्मक संकल्पनांचे काटेकोर व्याख्येत रूपांतर होण्यासाठी १९ वे शतक उजाडावे लागले, जेव्हा वाइरस्ट्रास यांनी ‘सीमा’ संकल्पनेची व्याख्या दिली (डेल्टा व एप्सीलॉन चिन्हे वापरून). पूर्णत्वासाठी गणितज्ञ किती श्रम घेतात हे यावरून स्पष्ट होते.
इवलीशी दिसणारी चिन्हेही या भाषेचे खास सौंदर्य असून खूप मोठा आशय व्यक्त करतात. प्रमाणित चिन्हे आणि त्यांचा अर्थ हा गणितविश्वात सर्वमान्य, सर्वज्ञात असतो. यामुळे गणिताची भाषा संक्षिप्त आणि अर्थसंपृक्त बनते. बीजगणितातील शालेय पुस्तकातील शाब्दिक गणिते आठवून पाहा. पानभर वर्णनात्मक गणित केवळ दोन-तीन सुटसुटीत समीकरणांमध्ये परावर्तित होते. दगडातला नको असलेला भाग दूर करून रेखीव शिल्प उरावे, तशीच ही गणिती प्रारूपे!
आकृत्या हेसुद्धा या भाषेचे महत्त्वाचे अंग. लांबलचक सिद्धता वाचून जे समजणार नाही ते आकृती पाहून एका दृष्टिक्षेपात समजू शकते. साधे आलेखही समस्यांचे वर्णन आणि विश्लेषण प्रभावीपणे मांडतात. गणिती मांडणीमुळे विज्ञानातले सिद्धान्त अधिक नेमकेपणे मांडता येतात आणि विश्वासार्ह बनतात. ‘अल्पाक्षरमसंदिग्धं सारवद्विश्वतोमुखम्’ असे सूत्राचे वर्णन केले जाते. सूत्र हे कमी अक्षरांचे, संदिग्ध नसलेले, सार सांगणारे, सर्वस्पर्शी असते, असा याचा अर्थ होतो. गणिती सूत्रांनाच नव्हे, तर पूर्ण गणिती भाषेलाच ते यथार्थ लागू पडते.
– प्रा. माणिक टेंबे
मराठी विज्ञान परिषद
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org