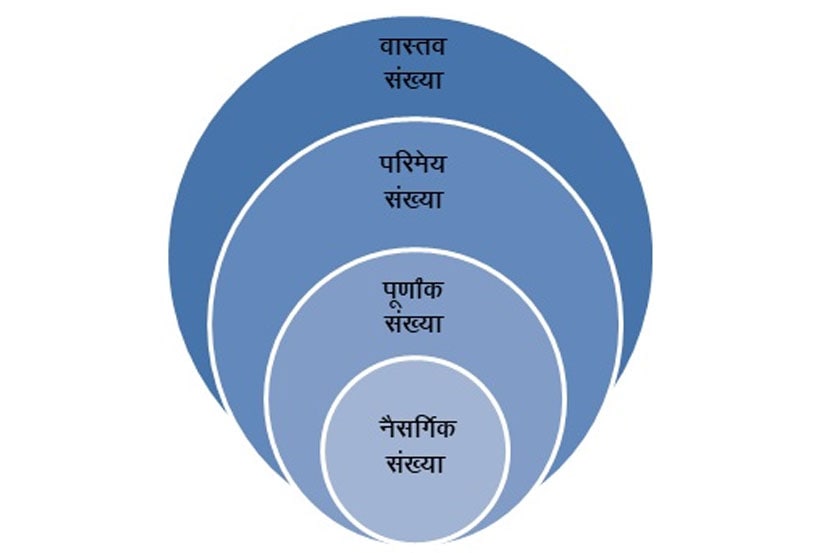
संख्यांचे विश्व पूर्णाकांपलीकडे विस्तारले, ते अगणित परिमेय (रॅशनल) व अपरिमेय (इर्रॅशनल) संख्या आणि त्या दोघांना एकत्र करणाऱ्या वास्तव संख्यासंचापर्यंत! परिमेय संख्या दोन पूर्णाक संख्यांच्या भागाकाराने अ/ब अशी व्यक्त होते ज्यात भाजक संख्या (ब) शून्य नसते. भाजक ब = १ असतो तेव्हा संख्या पूर्णाकी असते, तर भाजक अन्य शून्येतर संख्या असेल तर अपूर्णाकी. परिमेय संख्यांची विविध रूपे आपण व्यवहारात वापरतो. त्यातील काहींना पाव (१/४), अर्धा (१/२), पाऊण (३/४), सव्वा (१+१/४), अडीच (२+१/२) अशा विशेष संज्ञाही आहेत. भाजक १०० असलेली परिमेय संख्या शतमानाने टक्के (%) या चिन्हाने आपण दर्शवतो. छेदाचे मूळ अवयव फक्त दोन आणि/किंवा पाच असतील तर परिमेय संख्येला सान्त दशांश अपूर्णाकांचे रूप देता येते. छेदाचा एक जरी अवयव दोन किंवा पाचपेक्षा भिन्न असेल तर परिमेय संख्या अखंड आवर्ती (नॉन टर्मिनेटिंग रिकरिंग) दशांश स्वरूपात व्यक्त करता येते. जसे की, ५/४१ = ०.०१२१९५ १२१९५..
अपरिमेय संख्या दोन पूर्णाक संख्यांच्या गुणोत्तराने व्यक्त करता येत नाहीत. त्यांचे दशांशरूप अनंत अनावर्ती (नॉन टर्मिनेटिंग नॉन रिकरिंग) स्वरूपात असते. उदाहरणार्थ, √२, √५ किंवा ७ चे घनमूळ. त्यांची निश्चित किंमत येत नसल्याने व्यावहारिक आकडेमोडीसाठी आसन्न म्हणजे जवळची किंमत उपयोगात आणली जाते. प्रारंभी भूमितीच्या मदतीने या संख्यांचे मूल्य काढले जाई, पण नंतर अंकगणिती पद्धतीही शोधल्या गेल्या. अपरिमेय संख्यांचे अस्तित्व प्राचीन संस्कृतींना कळले होते. भारतात इ.स.पूर्व ८०० मधील बौधायन शुल्बसूत्रांमध्ये √२ ची किंमत १ + १/३ + १/ (३ x ४) — १/(३ x ४ x ३४) अशी काढण्यात आली.
परिमेय आणि अपरिमेय संख्यांचे काही महत्त्वाचे गुणधर्म आहेत. ‘शून्य’ ही परिमेय संख्या बेरीज अविकारक आहे. म्हणजे कोणत्याही संख्येत शून्य मिळविले तर त्या संख्येच्या किमतीत बदल होत नाही. ‘एक’ ही संख्या गुणाकार अविकारक आहे. त्यामुळे एकने कोणत्याही संख्येला गुणल्यास तीच संख्या येते. शून्याने कोणत्याही संख्येला गुणले तर उत्तर शून्यच येते. कोणत्याही दोन परिमेय संख्यांची बेरीज, वजाबाकी, गुणाकार व दोन शून्येतर परिमेय संख्यांचा भागाकार या परिमेय संख्याच असतात. मात्र अपरिमेय संख्यांची बेरीज, वजाबाकी, गुणाकार अथवा भागाकार यामुळे मिळणाऱ्या संख्या अपरिमेय असतीलच असे नाही.
– -प्रा. दिलीप गोटखिंडीकर
मराठी विज्ञान परिषद,
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org
(लेखक प्रा. दिलीप गोटखिंडीकर यांनी निधन होण्यापूर्वी ‘कुतूहल’साठी लिहिलेला लेख.)