वाचकांस हे माहीत असावे की एखाद्या चौकोनाच्या फक्त भुजाच दिलेल्या असतील तर त्या चौकोनाचे क्षेत्रफळ काढता येत नाही; अशा चौकोनाला निश्चित क्षेत्रफळ नसते, कारण फक्त भुजांची लांबी माहीत असता त्यातून एकच एक चौकोन तयार होत नाही, तर वेगवेगळे चौकोन तयार होतात.
तथापि अशा चौकोनाचे चारही शिरोबिंदू एखाद्या वर्तुळावर असतील, म्हणजेच तो चक्रीय (सायक्लिक) चौकोन असेल, तर मात्र त्याचे क्षेत्रफळ काढता येते, ज्याचे सूत्र ब्रह्मगुप्तांनी आपल्या ‘ब्राह्मस्फुटसिद्धांत’ या ग्रंथात देऊन ठेवलेले आहे. समजा चक्रीय चौकोनाच्या भुजांची लांबी अ, ब, क, ड आहे. प्रथम त्याची अर्धपरिमिती काढायची. ती ‘स’ या अक्षराने दाखवली जाते; स=(अ+ब+क+ड)/२. या ‘स’चा उपयोग करून चक्रीय चौकोनाच्या क्षेत्रफळाचे मिळणारे सूत्र आहे,
![]()
.
ब्रह्मगुप्तांच्या सूत्रातील ‘अ’ची किंमत लहान लहान करत शून्य केली तर या प्रक्रियेतून तयार होणारा आकार त्रिकोण असेल आणि त्याचे क्षेत्रफळ ![]()
इतके असेल. हे सूत्र हेरॉन या गणितींनी पूर्वीच शोधले होते. जाता जाता, पंधराव्या शतकातील भारतीय गणिती परमेश्वर यांचा सिद्धांत पाहायला हरकत नाही; जर, अ, ब, क, ड या एखाद्या चक्रीय चौकोनाच्या भुजा असतील आणि ‘र’ ही जर त्याच्या परिवर्तुळाची त्रिज्या असेल तर,

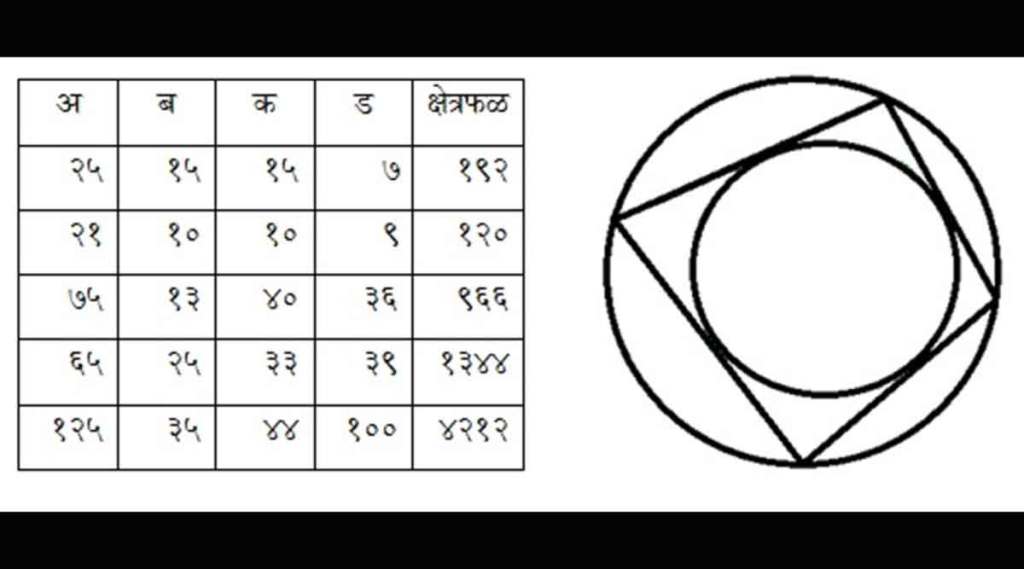
चक्रीय चौकोनाची आकृती काढणे हे फारसे अवघड नव्हे. मात्र त्याच्या चारही भुजांची लांबी पूर्णाकात हवी असल्यास ते निश्चितच एक गणिती आव्हान ठरेल. समजा अशा एखाद्या ‘पूर्णाकभुज’ चक्रीय चौकोनाचे क्षेत्रफळही पूर्णाकातच आले तर? अशा वैशिष्टय़पूर्ण चक्रीय चौकोनासच ब्रह्मगुप्त-चौकोन म्हटले जाते. अशा चौकोनाची परिमिती सम संख्या असते असेही सिद्ध करता येते. ब्रह्मगुप्त-चौकोनांची काही उदाहरणे दिलेल्या तक्त्यात पाहू. चौकोनाच्या भुजा अ, ब, क, ड या क्रमानेच घ्यायच्या आहेत.
ब्रह्मगुप्तांनी केलेल्या चक्रीय चौकोनाच्या कार्यावरून एक नियम सिद्ध करता येतो की जर त्या चौकोनाच्या भुजांना आतल्या बाजूने दुसरे एखादे वर्तुळ स्पर्श करत असेल (आकृती पाहा) तर त्या चौकोनाच्या क्षेत्रफळाचे सूत्र

इतके सोपे आणि सुंदर रूप धारण करते.