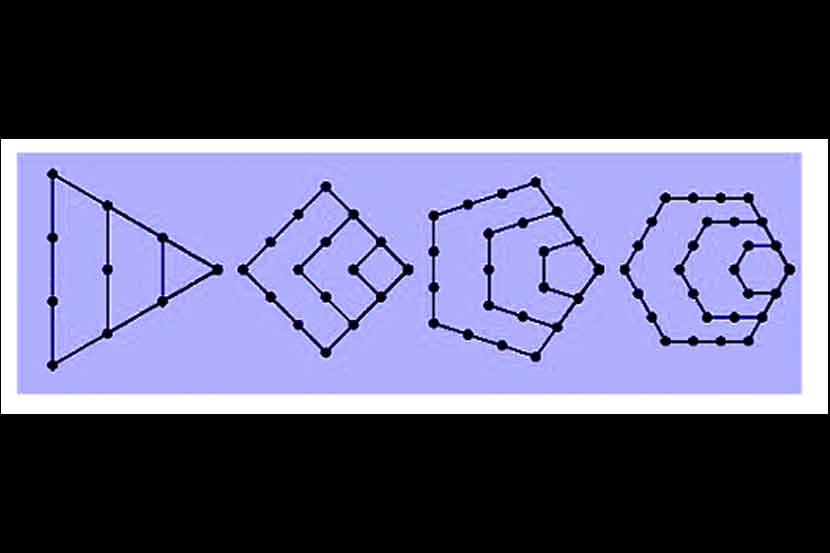
त्रिकोणी व चौरसाकार संख्यांच्या संकल्पनेच्या विस्ताराने उदयाला आल्या बहुकोनी (पॉलिगोनल) संख्या! समान अंतरावरील बिंदूंच्या रचनेद्वारे जर द्विमितीय सुसम बहुभुजाकृती मिळत असेल, तर त्या रचनेतील बिंदूंच्या संख्येला बहुकोनी संख्या म्हणतात. कोणत्याही बहुभुजाकृतीसाठी १ ही पहिली बहुकोनी संख्या मानतात. आकृतीत प्रत्येकी पहिल्या चार त्रिकोणी, चौकोनी, पंचकोनी आणि षट्कोनी संख्या दाखवल्या आहेत.
ज्या बहुकोनी संख्यांपासून ‘क’ बाजूंची (क : २ हून मोठी नैसर्गिक संख्या) बहुभुजाकृती तयार होते, त्यांना क-कोनी संख्या म्हणू. अशी ‘न’ क्रमांकाची क-कोनी संख्या
त्र(क-२)७न२-(क-४)७नत्न/२ या सूत्राने मिळते. उदा. तिसरी पंचकोनी संख्या शोधण्यासाठी या सूत्रात क=५ आणि न=३ ठेवावे. या सूत्रावरून बहुकोनी संख्यांचे अनेक गुणधर्म अभ्यासता येतात, त्यातील काही आपण पाहू.
‘न’वी पंचकोनी संख्या ही ‘न’पासून सुरू होणाऱ्या ‘न’ नैसर्गिक संख्यांची बेरीज असते. जशी, दुसरी पंचकोनी संख्या २+३=५ आहे. ‘न’व्या पंचकोनी संख्येची तिप्पट म्हणजे (३न-१)वी त्रिकोणी संख्या! उदा. दुसऱ्या पंचकोनी संख्येची (५ची) तिप्पट ही ३७२-१=५वी त्रिकोणी संख्या १५ आहे. षट्कोनी संख्या म्हणजेच विषम क्रमांकाच्या त्रिकोणी संख्या! १, ६, १५,… ही त्यांची क्रमिका.
फर्मा यांनी सन १६३८ मध्ये सांगितलेला बहुकोनी संख्यांचा सिद्धान्त त्यांच्याच नावाने अंकशास्त्रात प्रसिद्ध आहे. तो असा : कोणतीही नैसर्गिक संख्या ‘क’ किंवा त्याहून कमी क-कोनी संख्यांच्या बेरजेच्या स्वरूपात लिहिता येते. जसे की, कोणतीही नैसर्गिक संख्या ३ किंवा त्याहून कमी त्रिकोणी, ४ किंवा त्याहून कमी चौकोनी संख्यांच्या स्वरूपात लिहिता येते. उदाहरणार्थ, १७=१०+६+१ (३ त्रिकोणी संख्या), १७=१६+१ (२ चौकोनी संख्या), १७=१२+५ (२ पंचकोनी संख्या). १७७० साली हा सिद्धान्त लाग्रांज यांनी चौकोनी संख्यांसाठी, तर १७९६ साली गाऊस यांनी त्रिकोणी संख्यांसाठी सिद्ध केला. पण संपूर्ण सिद्धतेसाठी १८१३ सालाची वाट पाहावी लागली; त्यावर्षी महान फ्रेंच गणितज्ञ कोशी यांनी ती सिद्धता दिली.
दोन वेगवेगळ्या बहुभुजाकृतींशी संबंधित बहुकोनी संख्यांच्या संचात आढळणाऱ्या बहुकोनी संख्यांचा (उदा. त्रिकोणी-चौकोनी संख्या) प्रश्न ब्रह्मगुप्त-पेल समीकरणांद्वारे सोडवला जातो. असा प्रश्न तीन वेगवेगळ्या बहुभुजाकृतींसाठी सोडवणे फार कठीण आहे. उदा. त्रिकोणी-चौकोनी-पंचकोनी अशी एकच संख्या ज्ञात आहे : १! या संदर्भातील अटकळींवर गणितज्ञ संशोधन करत आहेत. बहुकोनी संख्यांप्रमाणेच आयत संख्या, समलंब चौकोनी संख्या, छ-आकाराच्या संख्या, घन संख्या, चतुष्फलकी (टेट्राहेड्रल) संख्या, शंक्वाकृती संख्या आदी संख्यांचा अभ्यासही रोचक आहे. – मुग्धा महेश पोखरणकर
मराठी विज्ञान परिषद,
संकेतस्थळ : www.mavipa.org
ईमेल : office@mavipamumbai.org