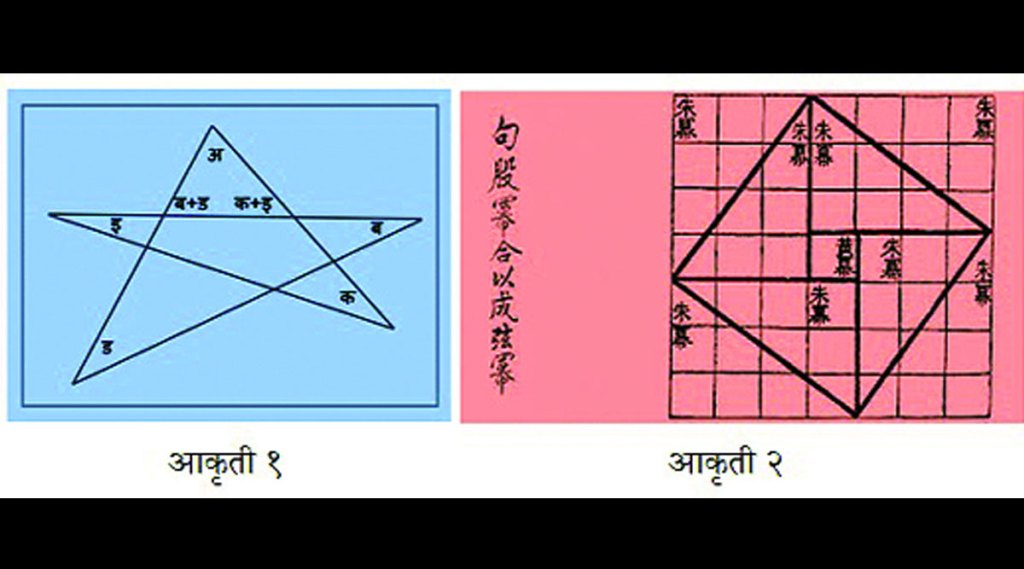
पाठ्यपुस्तकातल्या काही प्रमेयांच्या सिद्धता लहान असतात, तर काहींच्या तुलनेने मोठ्या असतात. सिद्धता लहान दिसली की मुले खूश होतात. पण तुम्हाला ठाऊक आहे का, की शाळा-महाविद्यालयातल्या अभ्यासक्रमातील अनेक प्रमेयांसाठी चक्क शब्द नसलेल्या सिद्धताही उपलब्ध आहेत? बिनशब्दांच्या सिद्धता आकृतीच्या स्वरूपात असतात. ही आकृती अशी असते की नुसती पाहिली तरी त्यातून सिद्धता समजते. उदाहरणार्थ, आकृती-१ पाहा. पंचकोनी चांदणीतील पाच कोनांची बेरीज १८० अंश असते, याची सिद्धता ही आकृती पाहाताच मनात उलगडत जाते. अशाप्रकारची आकृती म्हणजे बिनशब्दांची सिद्धता. काही वेळा स्थिर आकृतीऐवजी चलत्चित्र स्वरूपातही सिद्धता दिली जाते.
आकृतीत अनुरेखित असणाऱ्या सिद्धता प्राचीन काळापासून प्रचलित आहेत. पायथागोरसच्या प्रमेयाची अशी आकृती (आकृती-२), जिला ‘हसूयन-थु’ म्हणून ओळखले जाते आणि जिचा काळ ख्रिस्तपूर्व हजार वर्षे ते ख्रिस्तकालापर्यंत कुठचाही असू शकतो, ती आकृती अशा प्रकारच्या सिद्धतेचे प्राचीन उदाहरण म्हणता येईल. असे असले तरी, १९७० साली ‘अमेरिकन मॅथेमॅटिकल सोसायटी’ने जेव्हा तिच्या ‘मॅथेमॅटिक्स मॅगझिन’ आणि ‘कॉलेज मॅथेमॅटिक्स जर्नल’ यांमध्ये अशा सिद्धता नियमित छापण्यास सुरुवात केली तेव्हा या सिद्धतांना खरी मान्यता मिळाली अन् ‘बिनशब्दांची सिद्धता (प्रूफ विदाऊट वर्ड)’ हे नाव मिळाले. भूमिती, बीजगणित, त्रिकोणमिती, कलनशास्त्र, गणिती विश्लेषण या विषयांतील कित्येक प्रमेयांसाठी आता अशा सिद्धता शोधल्या गेल्या आहेत.
केवळ चित्र पाहून मनात सिद्धता उलगडण्याची प्रक्रिया कुठच्याही गणितप्रेमीसाठी विलक्षण आनंददायी असते. विद्यार्थ्यांना शाब्दिक सिद्धता लक्षात ठेवण्यापेक्षा दृश्यरूप लक्षात ठेवणे तुलनेत सोपे असते. आकृती पाहून स्वत: सिद्धता शोधणे हे रचनात्मक शिक्षणासाठी अनुकूल आहे. त्यामुळे गणित शिक्षणात या सिद्धतांचा वापर अतिशय प्रभावी ठरू शकतो. अर्थातच, अशा प्रकारच्या सिद्धतांना काही मर्यादा आहेत. उदाहरणार्थ, अनंत श्रेणीची सीमा काढण्याच्या सिद्धतांमध्ये अनंत पायऱ्या आकृतीत दाखवणे शक्य नसते. तिथे कल्पनेचाच वापर करावा लागतो. त्यामुळे शाब्दिक विधाने वापरून दिलेल्या सिद्धतांची जागा सर्व ठिकाणी बिनशब्दांच्या सिद्धता घेऊ शकणार नाहीत. शाब्दिक सिद्धता कुणीही वाचून समजून घेऊ शकेल, पण बिनशब्दांच्या सिद्धता समजण्यासाठी काही वेळा पुरेशी गणिती प्रगल्भता असणे गरजेचे आहे. अशा मर्यादा असल्या तरी या सिद्धता हा एक मोलाचा गणिती ठेवा आहे याबद्दल कुणाचेच दुमत असणार नाही. अभ्यासक्रमात असणाऱ्या अनेक प्रमेयांसाठी उपलब्ध बिनशब्दांच्या सिद्धता संग्रही ठेवून त्यांचा वापर शिक्षकांनी जरूर करावा. अशा सिद्धतांचे तक्ते बनवल्यास गणित प्रयोगशाळेचा तो एक महत्त्वाचा भाग होऊ शकतो. – प्रा. माणिक टेंबे
मराठी विज्ञान परिषद,
संकेतस्थळ : www.mavipa.org
ईमेल : office@mavipamumbai.org
लोकसत्ता आता टेलीग्रामवर आहे. आमचं चॅनेल (@Loksatta) जॉइन करण्यासाठी येथे क्लिक करा आणि ताज्या व महत्त्वाच्या बातम्या मिळवा.
First Published on May 28, 2021 12:10 am
