युक्लिड यांच्या ‘एलिमेण्टस्’ या ग्रंथातील भूमितीची रचना गृहीतकांवर आधारित आहे. सिद्धतेशिवाय स्वीकारलेली फक्त पाच गृहीतके आणि त्यानंतर कोणतेही प्रमेय ही पाच गृहीतके आणि आधी सिद्ध केलेली प्रमेये यांच्या आधारे सिद्ध करायचे, अशाप्रकारे या प्रतल भूमितीची मांडणी केली आहे. गणिती शाखेची अशी गृहीतकांवर आधारित रचना करण्याची कल्पनाही गणिती विश्वाला युक्लिडच्या भूमितीतून मिळालेली बहुमोल देणगी आहे. असे सर्व असले तरी त्यातल्या शेवटच्या गृहीतकाबद्दल २००० वर्षांहून अधिक काळ ते गृहीतक आहे, की प्रमेय म्हणून इतर गृहीतके वापरून त्याची सिद्धता देता येईल, अशा संभ्रमात गणितज्ञ होते हे तुम्हांला ठाऊक आहे का?
युक्लिडची मूळ गृहीतके अशी आहेत :
१) कुठच्याही दोन बिंदूंमधून जाणारी सरळ रेषा काढता येते.
२) रेषाखंड दोन्ही बाजूंनी कितीही दूर वाढवता येतो.
३) कोणताही केंद्रबिंदू आणि कितीही त्रिज्या असणारे वर्तुळ काढता येते.
४) कोणतेही दोन काटकोन हे एकरूप असतात.
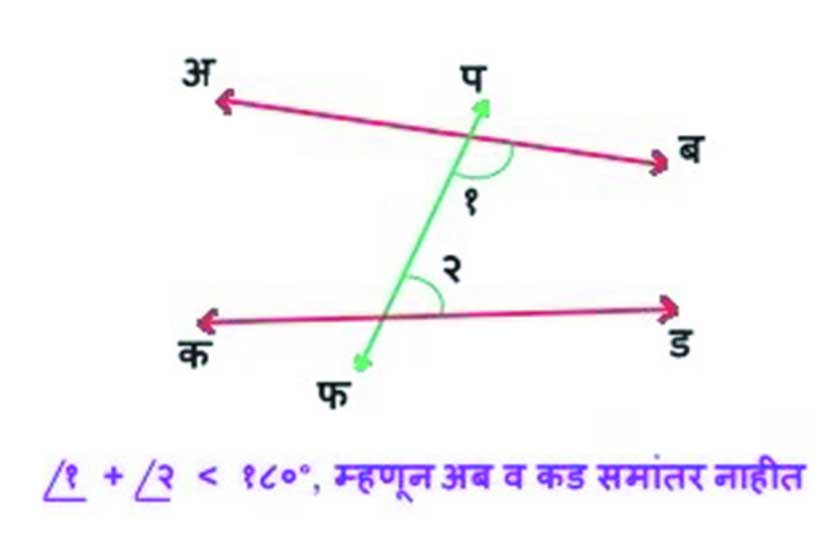
५) प्रतलातील दोन रेषांना तिसरी रेषा छेदत असेल आणि या तिसऱ्या रेषेने पहिल्या दोन रेषांशी एका बाजूला केलेल्या अंतर्कोनांची बेरीज दोन काटकोनांहून कमी असेल तर त्या बाजूला वाढवत नेल्यावर त्या दोन रेषा एकमेकींना छेदतात.
सदर गृहीतके वाचल्यावर पाचवे गृहीतक पहिल्या चारांहून मोठे, थोडे अवघड आणि प्रमेयाच्या विधानासारखे वाटते. त्यामुळे ते पहिली चार गृहीतके वापरून प्रमेय म्हणून सिद्ध करता येईल, असे गणितज्ञांना वाटले. तसे प्रयत्न सुरू झाले आणि सिद्धता सापडल्याचा चुकीचा दावासुद्धा अनेकदा केला गेला. टॉलेमी, प्रोक्लस, वॅलिस या गणितींनी अशा चुकीच्या सिद्धता दिल्याची नोंद इतिहासात आहे.
अठराव्या शतकात जॉन प्लेफेअर यांनी प्रतलावर ‘दिलेल्या रेषेला तिच्या बाहेरील बिंदूतून जास्तीत जास्त एक समांतर रेषा काढता येते.’ हे पाचव्या गृहीतकाशी समतुल्य असणारे अधिक सुटसुटीत विधान मांडले. हिल्बर्ट यांनी त्यांच्या युक्लिडच्या भूमितीवरील पुस्तकात हेच विधान पाचव्या गृहीतकाऐवजी वापरले आहे. अठराव्या शतकातले जेंडर यांनी ४० वर्षे प्रयत्न करून पाचवे गृहीतक हे ‘त्रिकोणाच्या तीन कोनांची बेरीज १८० अंश असते’ या विधानाशी समतुल्य असल्याचे सिद्ध केले. अखेरीस एकोणिसाव्या शतकात जर्मन गणितज्ञ कार्ल फ्रेडरिख गाऊस यांना हे गृहीतक इतर चार गृहीतके वापरून सिद्ध करता येणार नाही, हे स्पष्ट कळले. या प्रयत्नातून अखेरीस त्यांना अयुक्लिडीय भूमिती गवसली. पाचवे गृहीतक सिद्ध करण्याचे अयशस्वी प्रयत्नही नव्या भूमितीच्या अनोख्या विश्वाची नांदी ठरली.
– प्रा. माणिक टेंबे
मराठी विज्ञान परिषद,
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org