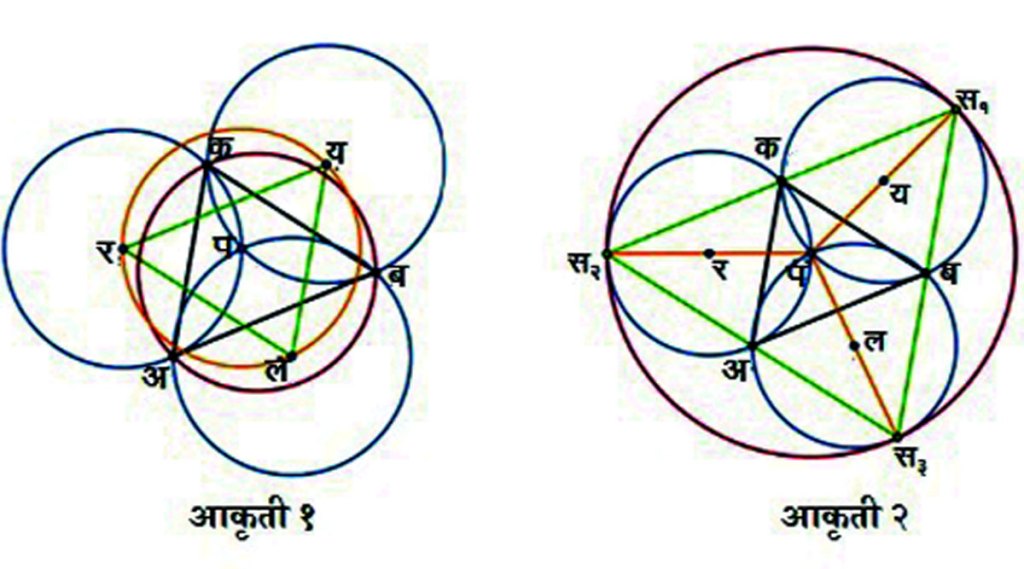
रॉजर जॉन्सन (सन १८९०-१९५४) यांनी ‘अमेरिकन मॅथेमॅटिकल मंथली’ या नियतकालिकात १९१६ साली हे प्रमेय मांडून त्याची सिद्धता दिली. प्रमेयाचे विधान असे : ‘‘त’ त्रिज्येची तीन एकरूप वर्तुळे एकमेकांना एका सामाईक बिंदूत छेदत असतील, तर जोडीच्या वर्तुळांच्या इतर तीन छेदनबिंदूंमधून जाणाऱ्या वर्तुळाची त्रिज्या ‘त’इतकीच असते.’ आकृती-१ मध्ये दाखवल्याप्रमाणे जॉन्सनचे प्रमेय मांडता येईल.
आकृती-१ मध्ये ‘त’ त्रिज्या असणारी तीन एकरूप वर्तुळे एकमेकांना ‘प’ बिंदूत छेदतात. तर ‘अ’, ‘ब’, ‘क’ या छेदनबिंदूंमधून जाणाऱ्या वर्तुळाची त्रिज्याही ‘त’इतकीच असेल. एवढेच नव्हे, तर ‘यरल’ त्रिकोणाच्या परिवर्तुळाची त्रिज्याही ‘त’इतकीच असते. हे आपल्या दृष्टीला जाणवते. पण सिद्ध कसे करायचे? पाहू या तर मग जॉन्सनची सिद्धता! इथे सोयीसाठी लघुकोन त्रिकोण निवडला आहे.
सर्व वर्तुळांच्या त्रिज्या एकरूप असल्याने आकृती-१ मध्ये ‘यर=अब’ आणि ‘यर॥अब’ हे सिद्ध करता येईल. त्यामुळे ‘यरअब’ हा समांतरभुज चौकोन होतो. म्हणून ‘अब=रय’ हे सिद्ध होते. त्याचप्रमाणे ‘बक=रल’; ‘अक=यल’ हेही सिद्ध करता येईल. त्रिकोण ‘अबक’ आणि त्रिकोण ‘रयल’ एकरूप होतात. म्हणून या त्रिकोणांची परिवर्तुळेही एकरूप होतात. ‘यरल’ त्रिकोणाच्या परिवर्तुळाचे केंद्र (‘प’) असल्यामुळे त्याची त्रिज्या इतर एकरूप वर्तुळांच्या त्रिज्येइतकीच असेल.
या प्रमेयाची सिद्धता त्रिकोणमितीच्या आधारे आणि सदिशांच्या (व्हेक्टर्स) आधारेही देता येते. या प्रमेयावरून एक उपप्रमेयही मिळते. तीन एकरूप वर्तुळे एका सामाईक बिंदूत छेदत असतील, तर जोडीच्या वर्तुळांचे इतर तीन छेदनबिंदू आणि तो सामाईक बिंदू यांपैकी प्रत्येक बिंदू इतर तीन बिंदूंनी तयार झालेल्या त्रिकोणाचा लंबसंपात बिंदू असतो. उदा. वरील आकृती-१ मध्ये ‘प’ हा त्रिकोण ‘अबक’चा लंबसंपात बिंदू आहे. प्रयत्न करा हे सिद्ध करण्याचा!
यावर आधारित प्रतिपूरक (अँटिकॉम्प्लिमेण्टरी) वर्तुळांचा एक गुणधर्म गणितप्रेमींना नक्कीच आवडेल. आकृती-२ मध्ये दाखविल्याप्रमाणे हे मोठे वर्तुळ तिन्ही जॉन्सन वर्तुळांना स्पर्श करते. खासियत अशी की, या तिन्ही वर्तुळांची केंद्रे छेदनबिंदू ‘प’ आणि स्पर्शबिंदू ‘स१’, ‘स२’, ‘स३’ यांना जोडणाऱ्या रेषेवर असतात. ‘स१स२स३’ हा प्रतिपूरक त्रिकोण आणि त्रिकोण ‘अबक’ समरूप आहेत. यावरून प्रेरणा घेऊन डी. एन. मॅकेन्झी यांनी १९९२ मध्ये जॉन्सन प्रमेयाचे व्यापकीकरण केले. त्या प्रमेयाला ‘ट्रिक्वेट्रा (एकमेकांत गुंफलेले तीन समभुज वक्र) प्रमेय’ असे म्हणतात. जॉन्सनच्या मूळ प्रमेयातील तीन वर्तुळे विविध त्रिज्येची असतील, तर काय निष्कर्ष निघेल? – नीलिमा मोकाशी
मराठी विज्ञान परिषद
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org