मूळसंख्या म्हणजे काय हे आपल्याला माहीत आहे. धन पूर्णांकांच्या संचातील मूळसंख्या या अतिशय वैशिष्ट्यपूर्ण असून त्यांच्याविषयी जसे अनेक सिद्धांत आहेत, तसेच अद्याप सत्य वा असत्य अशा निश्चितपणे सिद्ध न झालेल्या काही अटकळी (कन्जक्चर्स) आहेत. अॅण्ड्रिका अटकळ ही अशांपैकीच एक. रोमानियातील बेब्स्-बोल्याई विद्यापीठातील प्राध्यापक डोरीन अॅण्ड्रिका यांनी सन १९९६ मध्ये आपल्या शोधनिबंधात ही अटकळ मांडली होती. सदर शोधनिबंध त्यांच्या विद्यापीठाच्या शोधपत्रिकेत प्रसिद्ध झाला होता. त्यांच्या या अटकळीवर अनेक गणितींनी काम केले, मात्र तिची सत्यासत्यता अद्याप उलगडलेली नाही.
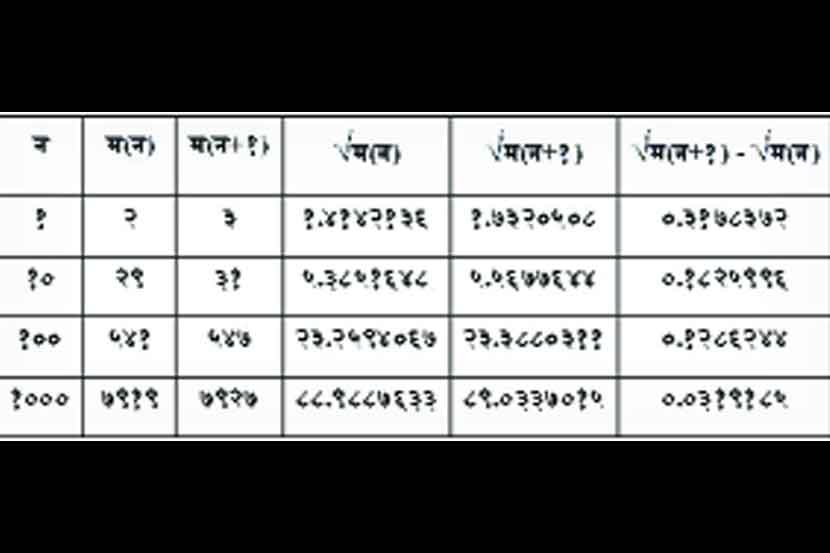
ती अटकळ अशी आहे : ‘न’ या कोणत्याही धन पूर्णांकासाठी ‘म(न)’ म्हणजे ‘न’व्या स्थानावर असलेली मूळसंख्या आहे असे मानू. (उदा. म(१) = २, म(२) = ३, म(३) = ५, म(४) = ७, इत्यादी). अॅण्ड्रिकांच्या अटकळीनुसार, ‘‘न’च्या कोणत्याही किमतीसाठी ‘म(न+१)’चे वर्गमूळ आणि ‘म(न)’चे वर्गमूळ यांच्यातील फरक एकपेक्षा कमी असतो’. म्हणजे लागोपाठच्या मूळसंख्यांच्या वर्गमुळांतील फरक एकपेक्षा कमी असतो. या संदर्भात सोबतचा प्रातिनिधिक तक्ता पाहावा.
‘न’च्या वाढत्या किमतीनुसार ‘न्न्म(न+१) – न्न्म(न)’ची किंमत कमीकमीच होत जाणार असा चुकीचा ग्रह मात्र या तक्त्यावरून करून घेऊ नये, कारण मूळसंख्यांचे एकूण वितरण काहीसे बुचकळ्यात टाकणारेच आहे. लागोपाठच्या मूळसंख्या कधी एकमेकींच्या अतिशय जवळ तर कधी एकमेकींपासून अतिशय दूर असतात (उदा. २३ व २९ यांच्यात तब्बल सहाचा फरक आहे तर २९ व ३१ यांच्यात अवघा दोनचा फरक आहे). त्यामुळे ‘न’च्या वाढत्या किमतीसह ‘न्न्म(न+१) – न्न्म(न)’च्या किमतीत अनेक चढउतार पाहायला मिळतात. मात्र ‘न’च्या कोणत्याही किमतीसाठी हा फरक एकपेक्षा मोठा झाल्याचे आढळलेले नाही. संगणकाच्या साहाय्याने ‘न’च्या १.३प्१०१६ इतक्या मोठ्या किमतीपर्यंत सदर अटकळीचा पडताळा घेतला आहे. अर्थात ‘न’च्या कितीही मोठ्या किमतीपर्यंत पडताळा घेतला तरी त्यातून ही अटकळ सिद्ध होत नाही; आणि म्हणूनच अनेक गणितज्ञ आजही हिच्यावर संशोधन करत आहेत. रिमानचे परिकल्पन (हायपोथेसिस) सत्य असल्याचे मानून अॅण्ड्रिकांची अटकळ सिद्ध करण्याचे प्रयत्नही चालले आहेत. – प्रा. सलिल सावरकर
मराठी विज्ञान परिषद
संकेतस्थळ : www.mavipa.org
ईमेल : office@mavipamumbai.org