गणितात आणि संख्याशास्त्रात पुढील चार मध्यांची (मीन) मूल्ये अतिशय महत्त्वाची भूमिका पार पाडतात : अंकगणिती (अॅरिथमेटिक) मध्य – अम, भौमितिक (जॉमेट्रिक) मध्य – भम, संवादी (हार्मोनिक) मध्य – सम, आणि वर्गमध्य (क्वाड्रॅटिक किंवा रूट मीन स्क्वेअर) – वम. सोयीसाठी अ आणि ब या दोन धन वास्तव संख्या घेतल्यास, अम = (अ+ब)/२; भम = (अप्ब)१/२; सम = २/(१/अ+१/ब) आणि वम = [(अ२+ ब२)/२]१/२. दोनपेक्षा अधिक धन वास्तव संख्यांसाठी या सूत्रांचे सहज व्यापकीकरण वापरता येते.
या मूल्यांना पुढील असमानता (इनइक्वॅलिटी) जोडते : वम > अम > भम > सम. बीजगणितीय आणि भौमितिक पद्धतींनी हे सिद्ध करता येते. यातील अम > भम ही असमानता इष्टतमीकरण (ऑप्टिमायझेशन) सिद्धांतात आणि एकूण गणितात पायाभूत मानली जाते.
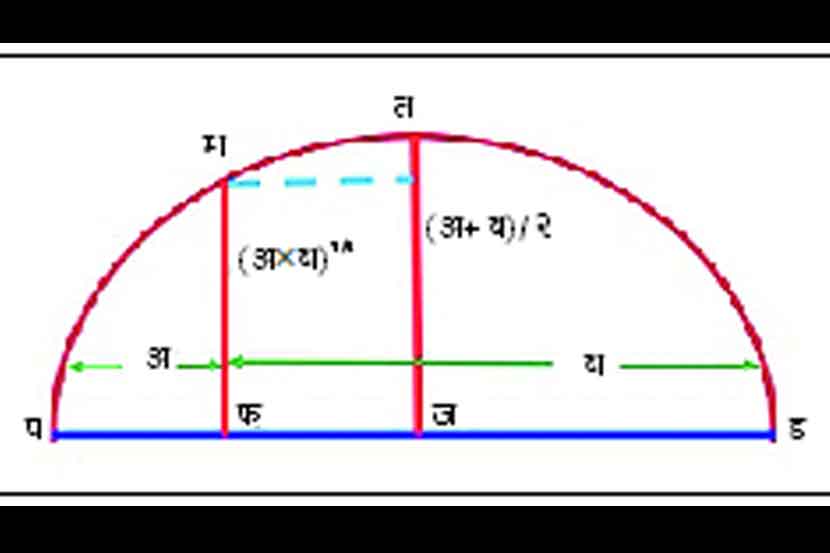
दोन मूल्यांसाठी अम > भम आकृतीमध्ये दिली आहे. त्यात पफ हा अ लांबीचा आणि फड हा ब लांबीचा रेषाखंड असून त्यांचा मध्यबिंदू ज आहे. पज = जड = (अ+ब)/२. ज केंद्रबिंदू घेऊन जप किंवा जड त्रिज्येचे अर्धवर्तुळ काढले आहे. फम आणि जत हे पड वरील लंब अर्धवर्तुळाला मिळतात. त्रिज्या जत = त्रिज्या पज = (अ+ब)/२. पायथागोरसचे प्रमेय वापरून फम = (अप्ब)१/२ हे सिद्ध करता येते. त्यावरून रेषाखंड जत > रेषाखंड फम, म्हणून अम > भम हे सिद्ध होते.
अम > भम या असमानतेच्या आधारे स्थापत्यशास्त्र, विद्युत अभियांत्रिकी, जहाज बांधणीसारख्या अनेक क्षेत्रांतील क्लिष्ट समस्या सोडवणासाठी भौमितिक प्रायोजन (जॉमेट्रिक प्रोग्रामिंग) ही विशेष ज्ञानशाखा विकसित झाली आहे. उदाहरणार्थ, विद्युत मनोऱ्याची उंची (ह), दोन मनोऱ्यांमधील वीज वाहून नेणाऱ्या तारेची लांबी (ल) आणि तारेचा तणाव (त) किती असावा ज्यायोगे त्यांना लागू असलेल्या विद्युत अभियांत्रिकीच्या नियमांत राहून किमान खर्च येईल, असे उत्तर प्रत्यक्षात काढावे लागते. समजा ख = २.२८६२४७१०८ ह(०.६) ल(-१) हे खर्च-फल (कॉस्ट फंक्शन) आहे आणि [१.१३१७प्१०८त२ + १.८९७७१०(-७)ल२] ख् १, [१०.२३७५ल२ + ३५ह(-१)] ख् १, ल > ०, त > ० आणि ह > ० अशा तांत्रिक मर्यादा (कंस्ट्रेंटस्) आहेत, तर खर्चाचे किमान मूल्य भौमितिक प्रायोजनाची पद्धत देते. त्याचे समुचित एककांत इष्टतम उत्तर, ल = ४०२, ह = २१.४ आणि त = २,२५८ आणि ख = ३५,६८,३०० आहे. साधी असमानता किती प्रभावी व दूरगामी ठरू शकते हे अचंबित करते. – डॉ. विवेक पाटकर मराठी विज्ञान परिषद,
संकेतस्थळ : www.mavipa.org
ईमेल : office@mavipamumbai.org