कुतूहल : रॅमसे संख्या खेळ

मनोरंजक गणिती खेळांमधला साधा सोपा वाटणारा परंतु अतिशय महत्त्वाच्या प्रमेयावर आधारलेला एक खेळ म्हणजे ‘रॅमसे संख्या’ खेळ होय. या खेळाचा पाया म्हणजे रॅमसे प्रमेय! अल्पायुषी ब्रिटिश तत्त्वज्ञ व गणितज्ञ फ्रँक रॅमसे (२२ फेब्रुवारी १९०३-१९ जानेवारी १९३०) यांनी पहिल्यांदा हे प्रमेय सिद्ध केले. चयनशास्त्र (कॉम्बिनेटोरिक्स) आणि आलेख सिद्धांत (ग्राफ थिअरी) या क्षेत्रांत रॅमसे प्रमेय आणि त्यावर आधारित रॅमसे सिद्धांत महत्त्वाची भूमिका बजावतात.

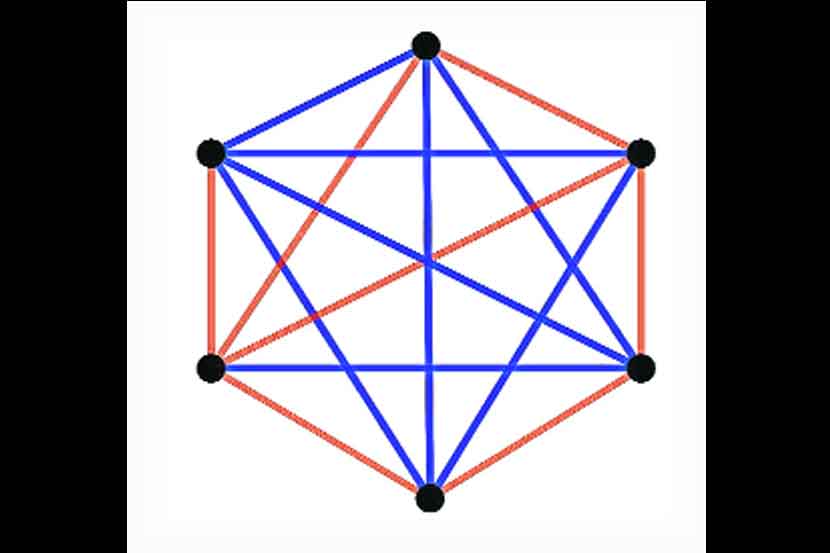
‘न’ शिरोबिंदू असलेल्या आलेखात जर प्रत्येक जोडीतील दोन शिरोबिंदू एकमेकांना रेषेने जोडलेले असतील तर त्याला ‘संपूर्ण आलेख’ (कम्प्लीट ग्राफ) म्हणतात. अशा आलेखात जर शिरोबिंदूंची संख्या पुरेशी जास्त असेल आणि त्यातील प्रत्येक रेषा दोनपैकी (उदा. लाल आणि निळा) एका रंगाने रंगवल्यावर, ‘स’ शिरोबिंदूंचा सर्व लाल रेषांचा किंवा ‘क’ शिरोबिंदूंचा सर्व निळ्या रेषांचा संपूर्ण उपआलेख (सबग्राफ) मिळेल असे रॅमसे प्रमेय सांगते. यासाठी लागणाऱ्या मूळ आलेखातील शिरोबिंदूंच्या लहानात लहान संख्येला रॅमसे संख्या र(स,क) म्हणतात. इथे ‘स’ व ‘क’ या नैसर्गिक संख्या आहेत. जर सहा शिरोबिंदूंचा संपूर्ण आलेख घेऊन त्यातील रेषा आलटून पालटून दोनपैकी एक खेळाडू लाल रंगाने व दुसरा खेळाडू निळ्या रंगाने रंगवत असेल तर जो खेळाडू पहिल्यांदा आपल्याकडील रंगाने त्रिकोण (३ शिरोबिंदूंचा संपूर्ण उपआलेख) पूर्ण करील तो खेळाडू विजयी ठरतो. इथे सहा ही शिरोबिंदूंची संख्या र(३,३) एवढी असल्याने रॅमसे प्रमेयावरून कोणतातरी एक खेळाडू जिंकेल हे नक्की करता येईल, परंतु जर सहाहून कमी शिरोबिंदू असलेला संपूर्ण आलेख घेतला व खेळाडू योग्य तर्क वापरून खेळत असतील तर हा खेळ अनिर्णित राहील.

लहान मुलांना सोपे वाटावे यासाठी आधीच त्रिकोण किंवा चौकोन असे आकार निश्चित करून रॅमसे संख्या खेळ खेळला जातो. आपल्या रंगाचा संपूर्ण उपआलेख बनवताना दुसऱ्याला तसे करण्यापासून रोखणे अशी कसरत खेळात चुरस तसेच रंगत आणते. एखाद्या कार्यक्रमात निमंत्रित करण्यासाठी पाहुण्यांची लहानात लहान संख्या किती असावी, जेणेकरून त्यातील काही पाहुणे एकमेकांना ओळखत असतील किंवा ओळखत नसतील, अशा प्रश्नांचे उत्तर काढण्याचा खेळ म्हणूनही रॅमसे संख्या खेळ प्रसिद्ध आहे. थोडक्यात रॅमसे सिद्धांत एखाद्या संरचनेत किंवा प्रणालीत किमान किती घटक असावेत, जेणेकरून निर्देशित केलेला गुणधर्म अवश्य पाळला जाईल, याबाबत मार्गदर्शन करतो. रॅमसे सिद्धांताचे विस्तारित रूप गोंधळाच्या स्थितीत क्रमवारी लावून नियंत्रण स्थापित करते. त्यामुळे संगणकशास्त्राशिवाय व्यवस्थापनशास्त्रातही त्याचा उपयोग होतो. –   मुक्ताई मिलिंद देसाई मराठी विज्ञान परिषद,

संकेतस्थळ : www.mavipa.org       

ईमेल : office@mavipamumbai.org