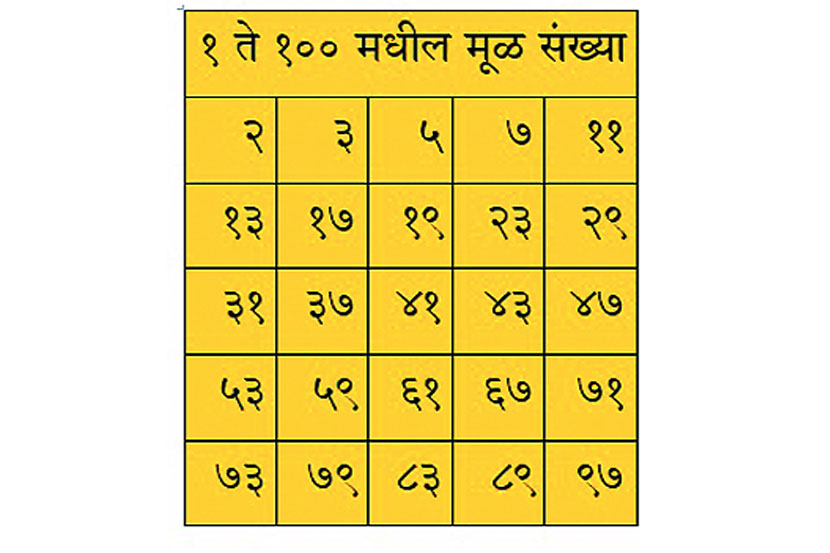
तुम्हाला माहीतच असेल, वर्तुळाचे आपण दोन, तीन, चार इत्यादी समान भाग सहज करू शकतो. याचे कारण म्हणजे वर्तुळ हे ३६० अंशांचे असते आणि ३६० चे दोन, तीन, चार.. समान भाग सहज होऊ शकतात. ज्या संख्येचे तिच्याहून लहान अशा दोन संख्यांच्या गुणाकाराच्या स्वरूपात अवयव काढता येतात, तिला संयुक्त संख्या (कॉम्पोझिट नंबर) म्हणतात. उदाहरणार्थ ४, १२, २४, ३६० इत्यादी. मात्र काही संख्यांचे अशाप्रकारे अवयव पाडता येत नाहीत. त्यांना फक्त एक आणि ती संख्या स्वत: अशा दोनच संख्यांनी पूर्ण भाग जातो. अशा संख्या म्हणजे अविभाज्य किंवा मूळ संख्या (प्राइम नंबर्स); उदा. २, ३, ५, ७, ११ इत्यादी.
युक्लिडच्या ‘एलिमेंट्स’ या ग्रंथातले अविभाज्य संख्यांसंबंधीचे दोन मुख्य सिद्धान्त असे आहेत : (१) १ पेक्षा मोठी प्रत्येक पूर्णाक संख्या ही एकतर अविभाज्य असते किंवा तिला अविभाज्य संख्यांच्या गुणाकाराच्या स्वरूपात एकमेव पद्धतीने लिहिता येते. (२) अविभाज्य संख्या अनंत आहेत.
या गुणधर्मामुळेच म्हणता येईल की, पूर्णाक संख्यांची इमारत अविभाज्य संख्यांच्या पायावर उभी आहे म्हणून अंकशास्त्रात अविभाज्य संख्यांच्या अभ्यासाला अनन्यसाधारण महत्त्व आहे. मात्र, अविभाज्य संख्यांच्या मांडणीतील सहसंबंध शोधणे अवघड आहे. ज्यातून केवळ अविभाज्य संख्या नेहमी मिळतील असे एखादे सूत्र पदावली स्वरूपात मिळत नाही. अविभाज्य संख्या शोधण्यासाठी एरातोस्थेनिसच्या चाळणी पद्धतीपासून ते अलीकडे संगणकावर आधारित अनेक पद्धती विकसित झाल्या आहेत. सध्या ज्ञात असलेली सर्वात मोठी अविभाज्य संख्या २,२३,३८,६१८ अंकी असून ती (२७४,२०७,२८१ – १) अशी आहे.
आयआयटी-कानपूरच्या मंनिन्द्र अग्रवाल, नीरज कयाल, नितीन सक्सेना या तीन संशोधकांनी २००२ साली अशी प्रचंड मोठी संख्या अविभाज्य आहे का, हे तपासण्यासाठी सुबक चाचणी विकसित करून भारतीयांना अभिमानास्पद अशी कामगिरी केली आहे. ती आता ‘एकेएस पद्धत’ या नावाने म्हणजे त्यांच्या आडनावाचे इंग्रजीतील पहिले अक्षर घेऊन तयार केलेल्या लघुनावाने ओळखली जाते.
दोन संख्यांचा गुणाकार करण्यापेक्षा एखाद्या मोठय़ा संख्येचे मूळ अवयव पाडणे हे तुलनेने कठीण असते. या वस्तुस्थितीचा वापर गुप्तसंदेशशास्त्र, संदेशवहनशास्त्र, आर्थिक व्यवहार व ‘पासवर्ड’ची सुरक्षा यासाठी केला जातो. त्यामुळेच संख्यांचे मूळ अवयव पाडणे यास खूप महत्त्व प्राप्त झाले आहे.
– प्रा. श्रीप्रसाद तांबे
मराठी विज्ञान परिषद
संकेतस्थळ : www.mavipa.org
ईमेल : office@mavipamumbai.org
टीप : ‘अविभाज्य संख्या’ या शीर्षकाखाली बुधवार- ३ फेब्रुवारी रोजी पूर्वप्रकाशित मजकूरच पुन्हा प्रसिद्ध झाला असल्याने तो शीर्षक व चित्राशी विसंगत आहे. यामागील तांत्रिक तसेच मानवी चूक दुरुस्त करण्यासाठी या अंकात, पुन्हा योग्य मजकूर देत आहोत.
लोकसत्ता आता टेलीग्रामवर आहे. आमचं चॅनेल (@Loksatta) जॉइन करण्यासाठी येथे क्लिक करा आणि ताज्या व महत्त्वाच्या बातम्या मिळवा.
First Published on February 4, 2021 12:07 am
