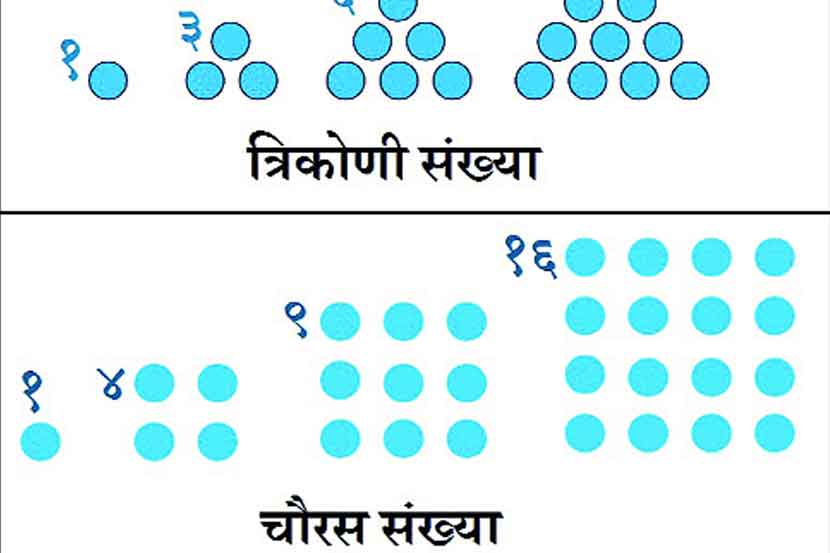
आकृत्या व संख्या या गणिताच्या दोन महत्त्वाच्या अंगांच्या सुंदर मिलाफाचे उदाहरण म्हणजे- त्रिकोणी (ट्रँग्युलर) व चौरसाकार (स्क्वेअर) संख्या! एक वा त्याहून जास्त समान अंतरावरील बिंदूंच्या रचनेने समभुज त्रिकोण तयार करता आला, तर त्याच्या मांडणीसाठी लागणाऱ्या बिंदूंची एकूण संख्या म्हणजे त्रिकोणी संख्या. ‘१’ ही पहिली त्रिकोणी संख्या मानली जाते.
पहिल्या ‘न’ नैसर्गिक संख्यांची बेरीज म्हणजेच ‘न’वी त्रिकोणी संख्या. त्यामुळे ‘न’ क्रमांकाची त्रिकोणी संख्या
त्रन७(न+१)त्न/२ या सूत्राने मिळते. उदा. चौथी त्रिकोणी संख्या = (४ ७५) / २ = १०. यावरून १, ३, ६, १०, १५,… अशी त्रिकोणी संख्यांची क्रमिका मिळते. हे सूत्र गाऊस यांनी शोधले असे म्हणतात; मात्र इ.स.पूर्व पाचव्या शतकात पायथागोरिअन पंथाच्या मंडळींना या संख्यांबाबत माहिती असल्याचे आढळते.
(न+१) खेळाडूंपैकी प्रत्येक खेळाडूने उरलेल्या प्रत्येक खेळाडूबरोबर प्रत्येकी एकच सामना खेळल्यास एकूण सामन्यांची संख्या ‘न’वी त्रिकोणी संख्या असते. जसे, वरील नियमानुसार ५ खेळाडूंचे एकूण १० (चौथी त्रिकोणी संख्या) सामने होतात. पहिल्या ‘न’ त्रिकोणी संख्यांची बेरीज त्रन७(न+१)७(न+२)त्न/६ या सूत्राने मिळते; त्यातून मिळणाऱ्या संख्या या चतुष्फलकी (टेट्राहेड्रल) संख्या! उदाहरणार्थ, पहिल्या ३ त्रिकोणी संख्यांची बेरीज १०, जी तिसरी चतुष्फलकी संख्या आहे. प्रत्येक सम परिपूर्ण संख्या त्रिकोणी संख्या असते. प्रत्येक त्रिकोणी संख्येला एकतर ३ ने नि:शेष भाग जातो, किंवा ९ ने भागल्यावर १ बाकी उरते. कोणत्याही चार वेगवेगळ्या त्रिकोणी संख्या भूमितीय श्रेढीत असू शकत नाहीत, ही अटकळ सत्य असल्याचे सिद्ध झाले आहे. ज्या त्रिकोणी संख्यांचा क्रमांक हाही त्रिकोणी संख्या असतो, त्यांना ‘दुहेरी त्रिकोणी संख्या’ म्हणतात. उदाहरणार्थ, १ ही पहिली त्रिकोणी संख्या; ६ ही तिसरी त्रिकोणी संख्या, कारण ३ हीसुद्धा त्रिकोणी संख्या आहे.
चौरसाकार संख्या म्हणजे पूर्ण वर्ग संख्या (पूर्णांकांचे वर्ग). त्यामुळे ‘न’वी चौरसाकार संख्या न२ असते. उदाहरणार्थ, १, ४, ९, १६, २५,… या संख्यांएवढ्या समान अंतरावरील बिंदूंच्या रचनेतून चौरस तयार होतो, म्हणून त्यांना चौरसाकार संख्या म्हणतात. पहिल्या ‘न’ चौरसाकार संख्यांची बेरीज त्रन७(न+१)७(२न+१)त्न/६ एवढी असते. ‘न’ क्रमांकाची चौरसाकार संख्या पहिल्या ‘न’ विषम नैसर्गिक संख्यांच्या बेरजेएवढी असते. उदा. ४=१+३, ९=१+३+५. दोन लगतच्या त्रिकोणी संख्यांच्या बेरजेने चौरसाकार संख्या मिळतात; जसे की, १+३=४, ३+६=९, ६+१०=१६. अशा या लक्षवेधक त्रिकोणी व चौरसाकार संख्या! – मुग्धा महेश पोखरणकर
मराठी विज्ञान परिषद
संकेतस्थळ : www.mavipa.org
ईमेल : office@mavipamumbai.org