त्रिकोण ही स्थापत्यशास्त्रातील पूल किंवा इमारती अशा बांधकामांना मजबुती देणारी स्थिर रचना! असा महत्त्वाचा गुणधर्म असलेल्या त्रिकोणाच्या बाजू, कोन आणि विविध केंद्रबिंदू यांवर आधारित संशोधनातून अनेक प्रकारचे त्रिकोण मिळतात. ‘हेरोचा किंवा हेरॉन त्रिकोण’ हा त्यांपैकीच एक. इजिप्तमधील अलेक्झाण्ड्रिया येथील हेरो (इ.स. १०ते ७०) या यंत्रतज्ज्ञ व भूमितज्ज्ञ यांच्या नावाने तो ओळखला जातो. शालेय भूमितीत त्रिकोणाचे क्षेत्रफळ काढण्यासाठी असलेल्या सूत्रातून त्यांचा परिचय होतो. या सूत्रामुळे कोणत्याही आकाराचा भूभाग त्रिकोणांत विभागून त्या त्रिकोणांच्या बाजू मोजून क्षेत्रफळ काढणे शक्य असते. हेरो यांनी अन्य प्रतलीय आकृत्यांची क्षेत्रफळे व घनाकृतींची पृष्ठफळे काढण्याची सूत्रेही विकसित केली.
त्रिकोणाच्या बाजू अ, ब, क घेतल्या, तर अर्धपरिमिती स = (अ+ब+क)/२ येते. यावरून त्रिकोणाचे क्षेत्रफळ =
✔ [स(स-अ)(स-ब)(स-क)]. हेरो यांनी त्यांच्या ‘मेट्रिका’ या पुस्तकाच्या तीन भागांपैकी पहिल्या भागात या सूत्राची सविस्तर सिद्धता दिली आहे. या सूत्रावरून येणारे त्रिकोणाचे क्षेत्रफळ नेहमीच पूर्णाकी असेल असे नाही. मात्र हेरॉन त्रिकोणाचे वैशिष्टय़ म्हणजे, प्रत्येक बाजू पूर्णाक संख्या असतेच, पण क्षेत्रफळही पूर्णाक संख्या असते.
हेरॉन त्रिकोण तयार करण्याच्या अनेक पद्धती आहेत. त्यांपैकी दोन पुढीलप्रमाणे :
(१) हेरॉन त्रिकोणाच्या प्रत्येक बाजूला ‘न’ या नैसर्गिक संख्येने गुणून येणारा त्रिकोणही हेरॉन त्रिकोण असतो. उदाहरणार्थ, ५, ५, ६ या बाजूंच्या हेरॉन त्रिकोणाच्या प्रत्येक बाजूला ३ ने गुणून येणारा १५, १५, १८ या बाजूंचा त्रिकोण.
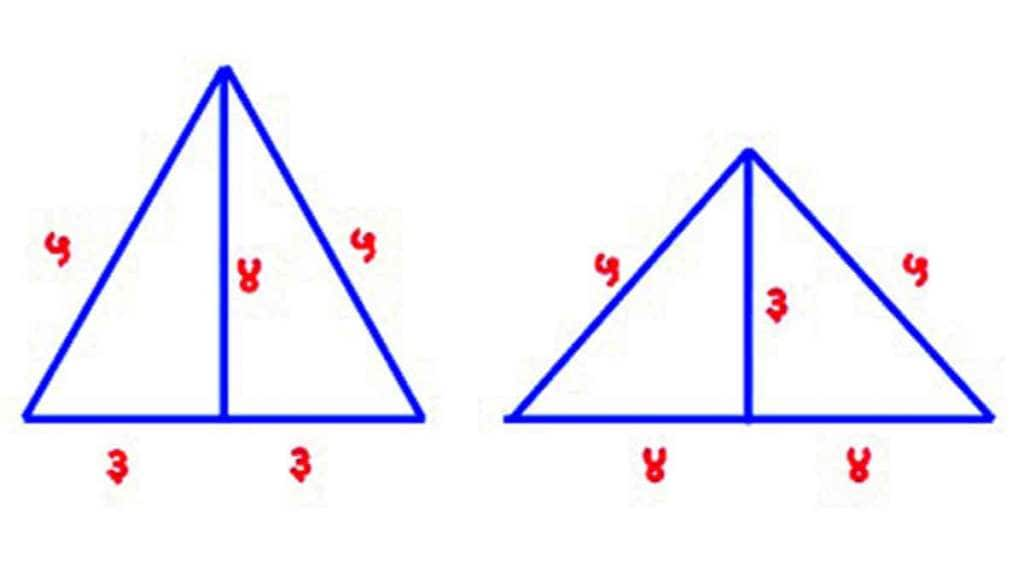
(२) ज्या काटकोन त्रिकोणांच्या बाजू पूर्णाक संख्या आहेत, असे एक बाजू सामाईक असणारे दोन काटकोन त्रिकोण एकमेकांना जोडून आकृतीत दाखवल्याप्रमाणे हेरॉन त्रिकोण मिळवता येतो. इथे ३, ४, ५ बाजू असलेले दोन काटकोन त्रिकोण दोन प्रकारे एकमेकांना जोडून ५, ५, ६ आणि ५, ५, ८ बाजूंचे हेरॉन त्रिकोण मिळतात. पायथागोरसच्या विविध त्रिकूटांवरून मोठय़ा संख्येत हेरॉन त्रिकोण तयार होतात.
हेरॉन त्रिकोणाची परिमिती नेहमी सम संख्या असते आणि अर्धपरिमिती कधीही मूळ संख्या नसते. कोणताही समभुज त्रिकोण हेरॉन त्रिकोण नसतो. पायथागोरस त्रिकूटांचे काटकोन त्रिकोण स्वत:ही हेरॉन त्रिकोण असतात. काही हेरॉन त्रिकोणांच्या बाजू क्रमागत संख्या असतात. जसे, (३, ४, ५), (१३, १४, १५). मात्र, कोणत्याही तीन क्रमागत संख्या हेरॉन त्रिकोणाच्या बाजू असतीलच असे नाही. तरी शोधा आणखी गुणधर्म अशा वैशिष्टय़पूर्ण हेरॉन त्रिकोणाचे!
– शोभना नेने
मराठी विज्ञान परिषद,
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org