नववर्ष २०२१च्या पहिल्या काही दिवसांतच- ‘चार भारतीय स्त्री वैमानिकांनी एअर इंडियाच्या एका विमानाचे सॅन फ्रॅन्सिस्को ते बेंगळूरु असे यशस्वी उड्डाण करून एका नव्या मार्गाचे उद्घाटन केले,’ ही बातमी आपण वाचली असेल. हा १४ हजार किलोमीटरचा प्रवास त्यांनी १७ तासांत पूर्ण केला. या उड्डाणाचे वैशिष्ट्य असे की, त्यांनी यासाठी उत्तर ध्रुवावरून येणारा मार्ग निवडला होता. आपण जगाचा नकाशा पाहिला तर ही दोन ठिकाणे नकाशाच्या दोन टोकांना दिसतील. तेव्हा हा प्रवास सरळसोट पश्चिम-पूर्व मार्गाने, अटलांटिक महासागरावरून, युरोप व आशिया खंडांवरून करता आला असता, फार तर पश्चिमेकडे जाऊन प्रशांत (पॅसिफिक) महासागर पार करून करता आला असता. त्यासाठी उत्तर ध्रुवावरून जाण्याची काय गरज होती? त्यात वेळ आणि इंधन खूप जास्त लागणार नाही का? असा प्रश्न पडणे साहजिकच आहे. पण घडते उलट!
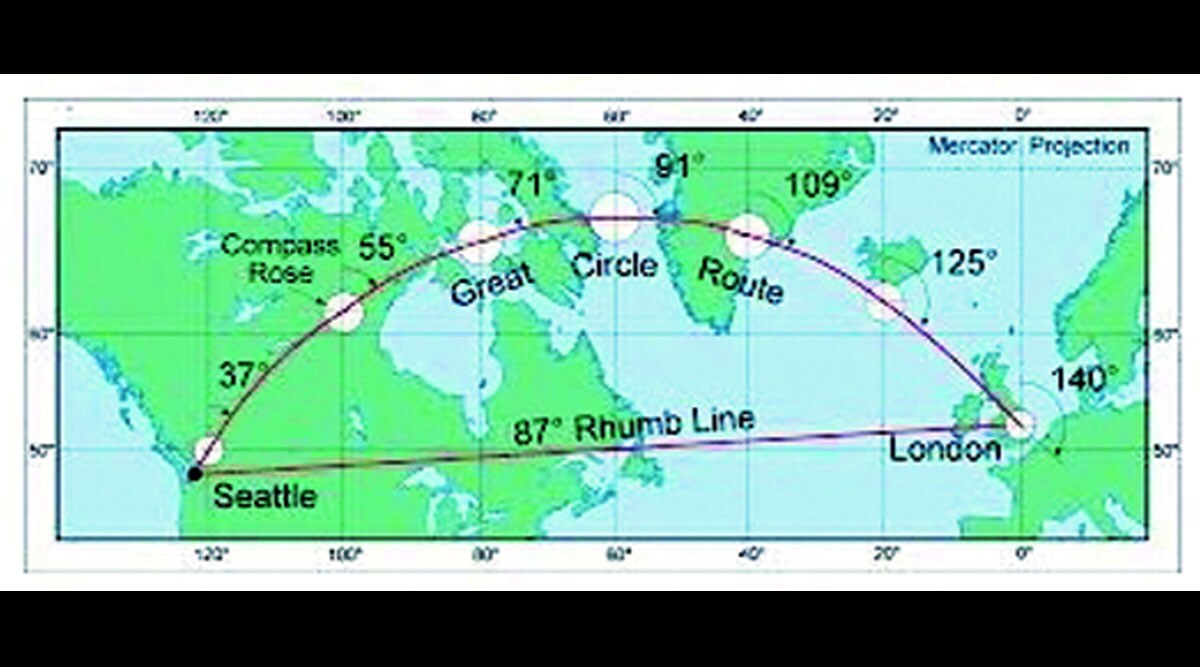
या प्रश्नाचे उत्तर समजून घेण्यासाठी लेखासह दिलेला नकाशा पाहा. यात सियाटल ते लंडन या स्थानांमधील सपाट नकाशावर काढलेला ‘सरळ’ मार्ग आणि पृथ्वीच्या गोलावर काढलेला ‘महावर्तुळ’ (ग्रेट सर्कल) मार्ग यांची तुलना दाखविलेली आहे. यांतील महावर्तुळ मार्गाचे अंतर सरळ मार्गापेक्षा १,२७६ किलोमीटरने कमी आहे. इथे जी रेघ सपाट पृष्ठभागावर ‘सरळ’ दिसते ती पृथ्वीच्या गोलावर वक्राकार दिसेल. याचे कारण पृथ्वीचा गोलाकार पृष्ठभाग आपण जेव्हा सपाट कागदावर दाखवू पाहतो तेव्हा भूभागांचे आकार ‘ताणले’ जातात आणि अंतरांचा व दिशांचा अंदाज अचूकपणे करता येत नाही. त्यासाठी गोलीय त्रिकोणमितीचा (स्फीरिकल ट्रिगॉनॉमेट्री) वापर करावा लागतो.
आपण शाळेत जी भूमिती किंवा त्रिकोणमिती शिकतो, ती सपाट पृष्ठभागावरची असते. त्रिकोणाच्या तीन कोनांची बेरीज १८० अंश असते हे ‘निर्विवाद सत्य’ फक्त सपाट प्रतलावरल्या त्रिकोणांना लागू पडते. गोलपृष्ठीय त्रिकोणाच्या तीन कोनांची बेरीज १८० पासून ५४० अंशांपर्यंत कितीही होऊ शकते. गोलीय त्रिकोणमिती आणि भूपृष्ठावरची स्थाननिश्चिती यांचा असा जवळचा संबंध असल्याने या त्रिकोणमितीचा उपयोग नाविक फार पूर्वीपासून करीत आले आहेत. कोलंबसाच्या काळात (पंधराव्या शतकातले दर्यावर्दी) दिवसाच्या लांबीवरून एखाद्या स्थानाचे अक्षांश काढण्यासाठी अशी त्रिकोणमिती वापरीत असत. नंतर सोळाव्या शतकाच्या उत्तरार्धात स्कॉटिश गणितज्ञ जॉन नेपियर यांनी या विषयाचा सखोल अभ्यास करून गोलपृष्ठावरची त्रिकोणमिती नाविकांकरिता अधिक सोपी करण्यासाठी मोलाची भर घातली. ‘जीपीएस’सारख्या आजच्या प्रगत स्थाननिश्चितीच्या प्रणालींमध्येसुद्धा गोलीय त्रिकोणमितीचा सहभाग अविभाज्य आहे. – कॅ. सुनील सुळे
मराठी विज्ञान परिषद, संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org