इ.स. १२व्या शतकादरम्यान लिओनार्दो फिबोनासी नावाचा इटालियन गणितज्ञ होऊन गेला. त्याच्या नावाने जी क्रमिका प्रसिद्ध आहे, त्यातील संख्यांना ‘फिबोनासी संख्या’ म्हणतात. फिबोनासीने या क्रमिकेची नोंद ‘लीबेर अबाची’ या पुस्तकात केली आहे. मात्र इ.स.पूर्व दुसऱ्या शतकातील पिंगलाचार्याच्या ‘छंद:सूत्र’ या भारतीय ग्रंथामध्येही या संख्यांची संकल्पना आढळते.
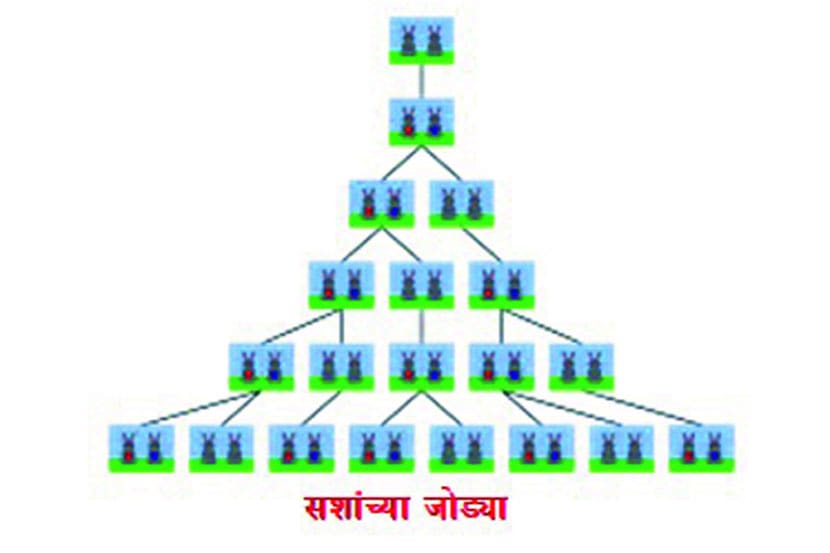
फिबोनासी संख्यांचा उगम पुढील गणिती प्रश्नातून झाला : समजा, एक नर आणि एक मादी अशी सशांची जोडी एका बंदिस्त जागी ठेवली. ही जोडी एका महिन्याने प्रजननक्षम होईल आणि त्यानंतर दर एका महिन्याने सशाच्या नर-मादी अशा एका जोडीला जन्म देत राहील. जन्माला आलेल्या प्रत्येक जोडीबाबत असेच घडत राहील, असेही मानू. हा क्रम असाच चालू राहिला, तर वर्षांच्या शेवटी सशांच्या किती जोडय़ा अस्तित्वात असतील? हा प्रश्न सोडवताना, पहिल्या आणि दुसऱ्या महिन्यात प्रत्येकी एकच जोडी असणार, तिसऱ्या महिन्यात ती जोडी एका जोडीला जन्म देणार, त्यामुळे एकूण दोन जोडय़ा होणार. याप्रमाणे सशांच्या जोडय़ांची संख्या दर महिन्याला १, १, २, ३, ५, ८, १३, २१, ३४, ५५, ८९, १४४,.. या क्रमिकेप्रमाणे असेल, असे फिबोनासीला आढळले. हीच ती फिबोनासी संख्या असलेली क्रमिका (सिक्वेन्स)! हिचे एक वैशिष्टय़ असे की, यातील तिसऱ्या संख्येपासून पुढची प्रत्येक संख्या आधीच्या दोन संख्यांच्या बेरजेइतकी आहे.
कोणतीही नैसर्गिक संख्या फिबोनासी संख्यांच्या बेरजेच्या स्वरूपात लिहिता येते. उदाहरणार्थ, ७ = २ + ५, ११ = ३ + ८. या संख्यांचे आणखी एक वैशिष्टय़ म्हणजे, दुसऱ्या फिबोनासी संख्येपासूनची कोणतीही फिबोनासी संख्या आणि तिच्या लगतची आधीची फिबोनासी संख्या यांचे गुणोत्तर (उदा., ५/३, ८/५, १३/८) हे वाढत्या संख्यांनुसार १.६१८ या संख्येच्या जवळ जाते. या संख्येला ‘सुवर्ण गुणोत्तर (गोल्डन रेशो)’ म्हटले जाते, कारण ते झाडांच्या फांद्या, पाने, फुलांच्या पाकळ्या, मृदुकाय प्राण्यांचे शंख या सुंदर दिसणाऱ्या नैसर्गिक गोष्टींच्या मापांच्या गुणोत्तरामध्ये अनेक वेळा दिसून येते. तसेच अनेक सुप्रसिद्ध चित्रे, शिल्पे, जगप्रसिद्ध इमारती, आल्हाददायक सांगीतिक कलाकृती यांच्या मितीतही सुवर्ण गुणोत्तर आढळते. त्यामुळे सुवर्ण गुणोत्तर आणि सौंदर्य यांच्यात नाते असल्याचे मानले जाते.
फिबोनासी संख्यांचा उपयोग गणितातील विविध शाखांमध्ये तसेच अर्थशास्त्र, भौतिकशास्त्र, संगणकशास्त्र आदी अनेक क्षेत्रांमध्येही केला जातो. शोधा तर त्यांचे आणखी उपयोग!
– मुग्धा महेश पोखरणकर
मराठी विज्ञान परिषद
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org