मध्ययुगीन भारतवर्षात जे अनेक नामवंत खगोलशास्त्रज्ञ आणि गणितज्ञ होऊन गेले त्यांच्यात ब्रह्मगुप्तांचे नाव आत्यंतिक आदराने घेतले जाते. इसवी सनाच्या सहाव्या शतकाच्या अखेरीस गुर्जर देश या प्रांतात जन्मलेल्या ब्रह्मगुप्तांचे ‘ब्राह्मस्फुटसिद्धांत’ आणि ‘खंडखाद्यक’ असे दोन ग्रंथ प्रसिद्ध आहेत. तत्कालीन परंपरेनुसार हे दोन्ही ग्रंथ पद्यात्मकच आहेत. ‘ब्राह्मस्फुटसिद्धांत’ पूर्णपणे आर्या वृत्तात रचलेला आहे. बाराव्या शतकातील विख्यात गणिती भास्कराचार्य यांनी ब्रह्मगुप्तांबद्दल ‘गणकचक्रचूडामणी’ असे कौतुकोद्गार काढले होते.
अंकगणित, बीजगणित, भूमिती, श्रेढीगणित, त्रिकोणमिती अशा गणिताच्या अनेक शाखा-उपशाखांमध्ये ब्रह्मगुप्तांनी सलील (लीलया) संचार केलेला दिसतो. शून्यासह ऋण संख्यांवरील गणिती क्रियांचे विवरण, अपूर्णांकांवरील विविध क्रिया, बीजगणितातील एकरेषीय आणि वर्गसमीकरणे सोडवण्याच्या पद्धती, १ पासून ‘न’ या कोणत्याही धन पूर्णांकापर्यंत असलेल्या संख्यांच्या बेरजेची तसेच त्यांच्या वर्गांच्या व घनांच्या बेरजेची सूत्रे, चक्रीय (सायक्लिक) चौकोनाच्या क्षेत्रफळाचे सूत्र, पायची आसन्न किंमत, काही त्रिमितीय आकारांची घनफळे, काटकोन त्रिकोणातील विविध कोनांच्या ‘ज्या’ फलाच्या किमती अशा अनेक गणित गोष्टींवर ब्रह्मगुप्तांचे काम दिसून येते. कोणत्याही कोनाच्या ‘साईन’ किमतीला ३४३८ ने गुणल्यावर येणारी किंमत ही त्या कोनाच्या ‘ज्या’ किमतीबरोबर असते. विविध कोनांच्या ‘ज्या’ किमती काढताना आंतररेखन (इंटरपोलेशन) पद्धत निर्माण करून तिचा वापर ब्रह्मगुप्तांनी केला होता. अशी पद्धत वापरणारे ते बहुतेक पहिले गणिती होते.
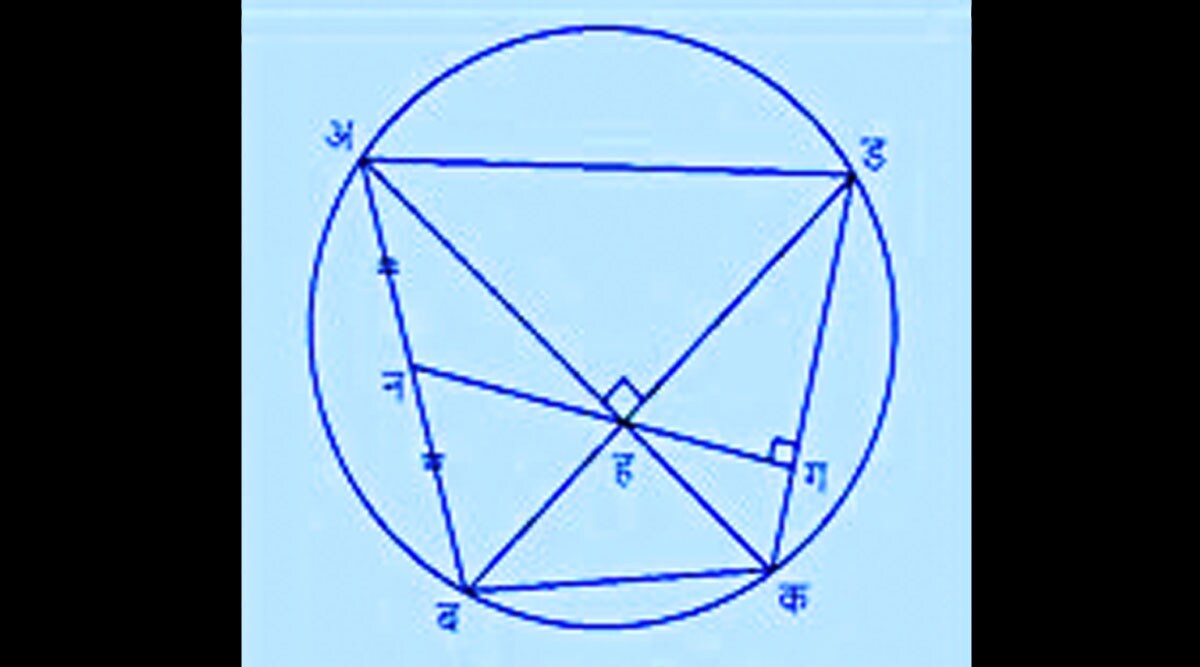
‘चक्रीय चौकोनाचे कर्ण जर एकमेकांस काटकोनात छेदत असतील तर त्यांच्या छेदनबिंदूतून जाणारी व चौकोनाच्या कोणत्याही एका भुजेस लंब असलेली रेषा समोरच्या भुजेची दुभाजक असते’ हा ब्रह्मगुप्तांचाच सिद्धांत आहे. आकृतीत ‘अबकड’ या चक्रीय चौकोनाचे ‘अक’ आणि ‘बड’ हे कर्ण ‘ह’ या बिंदूत एकमेकांना काटकोनात छेदतात. ‘कड’ भुजेवरील ‘हग’ हा लंब जर ‘ह’च्या दिशेने वाढवला तर तो ‘अब’ या भुजेस ‘न’ या बिंदूत छेदतो. ब्रह्मगुप्तांच्या नियमानुसार ‘अन’ = ‘नब’!
नक्ष२ + १ = य२ या प्रकारच्या अनिश्चित समीकरणांमध्ये ‘न’ची किंमत दिलेली असते. क्ष आणि य ही चलपदे असून त्यांच्या किमती पूर्णांकांतच काढायच्या असतात. जॉन पेल या गणितज्ञांच्या नावाने ओळखली जाणारी आधुनिक गणितातील ही समीकरणे पेल यांनी सोडवली नव्हती. मात्र, त्यांच्या जवळपास १००० वर्षे आधी जन्मलेल्या ब्रह्मगुप्तांनी ‘न’च्या विविध किमती घेऊन अशी समीकरणे सोडवली होती. किंबहुना, ही समीकरणे सोडवणारे जगातील पहिले गणिती ब्रह्मगुप्तच होते हे आज अनेकांनी मान्य केले आहे. भारतीय गणिताच्या सुवर्णकाळाचे ब्रह्मगुप्त हे निश्चितच एक महत्त्वाचे शिल्पकार होते. – प्रा. सलिल सावरकर
मराठी विज्ञान परिषद,
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org