‘चिओसचा हिप्पोकट्रीस’ म्हणून ज्ञात असलेला ग्रीक भूमितिविशारद खगोलतज्ज्ञदेखील होता. परंतु त्याच्याबद्दल फारशी माहिती उपलब्ध नसल्यामुळे वैद्यक क्षेत्रातील हिप्पोकट्रीसच्या तुलनेत तो प्रसिद्धीपासून वंचितच म्हणायला हवा. त्याचा जन्म इ.स.पूर्व ४७० मध्ये ग्रीसच्या चिओस (आताचे खोईस) बेटावर झाला. तिथल्याच एनॉपिडीज् नावाच्या खगोल/भूमितितज्ज्ञाच्या मार्गदर्शनाखाली त्याचे शिक्षण पार पडल्याचे सांगितले जाते. पायथागोरसच्या विचारांनी तो प्रभावित होता.
व्यापारी म्हणून कारकीर्दीची सुरुवात करणाऱ्या हिप्पोकट्रीसला व्यवसायात फसवणुकीला सामोरे जावे लागले. त्यावर दाद मागण्यासाठी तो अथेन्सला गेला. तिथे दीर्घकाळ वास्तव्य करणे भाग पडल्यामुळे तो तत्त्वज्ञान आणि भूमितीविषयक व्याख्यानांना उपस्थित राहू लागला. नंतर भूमितीचे शिक्षण देणारी शाळा सुरू करून तो तिथेच स्थायिक झाला. तत्कालीन भूमितीवरील पहिले पाठय़पुस्तक तयार करणारी व्यक्ती म्हणून त्याला मान दिला जातो. ‘एलिमेंट्स’ या युक्लिडच्या प्रसिद्ध पुस्तकासाठी हिप्पोकट्रीसने लिहिलेले याच शीर्षकाचे पुस्तक मूलस्रोत म्हणून वापरले गेले असावे असा अंदाज आहे. हिप्पोकट्रीसच्या ‘एलिमेंट्स’ने प्राचीन गणितींना त्यांच्या ज्ञानाची पद्धतशीर मांडणी करण्यासाठी उत्तम भाषा-माध्यम उपलब्ध करून दिले.
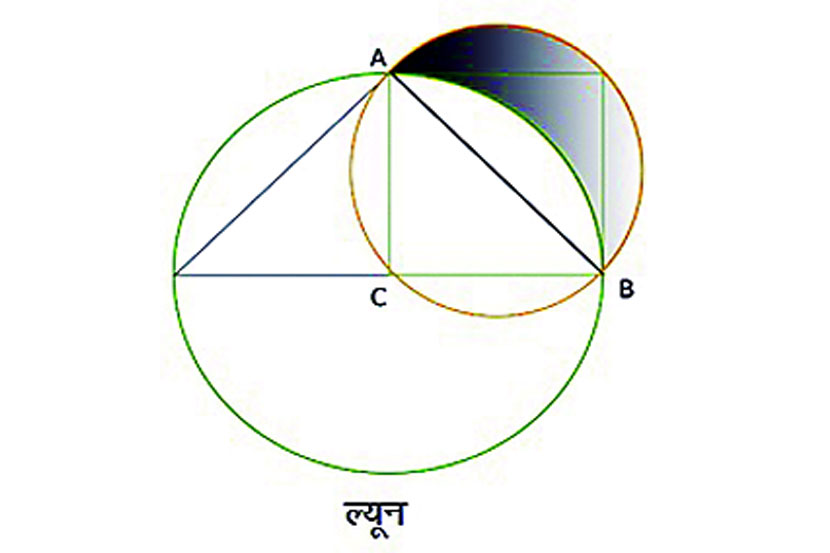
हिप्पोकट्रीसने कोनाचे त्रिभाजन आणि त्याच्याशी निगडित काही मूलभूत प्रश्नांविषयी काम केले. वर्तुळाचे चौरसात रूपांतर करण्याच्या प्रयत्नात असताना त्याने मांडलेली ‘ल्यून’ नावाची संकल्पना ‘ल्यून ऑफ हिप्पोकट्रीस’ म्हणून जगविख्यात आहे. त्याने एक अर्धवर्तुळ आणि एक पाववर्तुळ यांच्या परस्पर छेदातून तयार होणारी ल्यून तयार केली. वर्तुळाच्या दोन कंसांद्वारे बद्ध होऊन तयार झालेल्या आकाराचे सरळ रेषांच्या स्वरूपात क्षेत्रफळ काढले. वर्तुळाचे चौरसात रूपांतर करण्याविषयीचे प्रथम प्रमेय ते हेच! एखाद्या वर्तुळास विविध पाकळ्यांच्या आकारात विभाजित करून त्यांचे क्षेत्रफळ माहीत झाल्यास संपूर्ण वर्तुळाचे क्षेत्रफळ कळू शकते. याच प्रक्रियेस ‘क्वाड्रेचर ऑफ द सर्कल’ असेही म्हणतात, ज्याची मांडणी हिप्पोकट्रीसने केली.
हिप्पोकट्रीसने आणखीही दोन महत्त्वपूर्ण पद्धती दिल्या. एक म्हणजे, एखाद्या संख्येच्या घनमूळाची मांडणी भूमितीय पद्धतीने करणे; आणि दुसरी, एखाद्या समस्येची अप्रत्यक्ष सिद्धता देण्याची पद्धत (रिडक्शन मेथड). यात गणितीय समस्येचे सर्वसाधारण समस्येत रूपांतर करून विसंगतीतून सिद्धता साकारून सोप्या रीतीने मूळ समस्येचे उत्तर सापडते, अर्थात ‘प्रूफ बाय कॉन्ट्राडिक्शन’!
– शैलेश माळोदे
मराठी विज्ञान परिषद,
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org