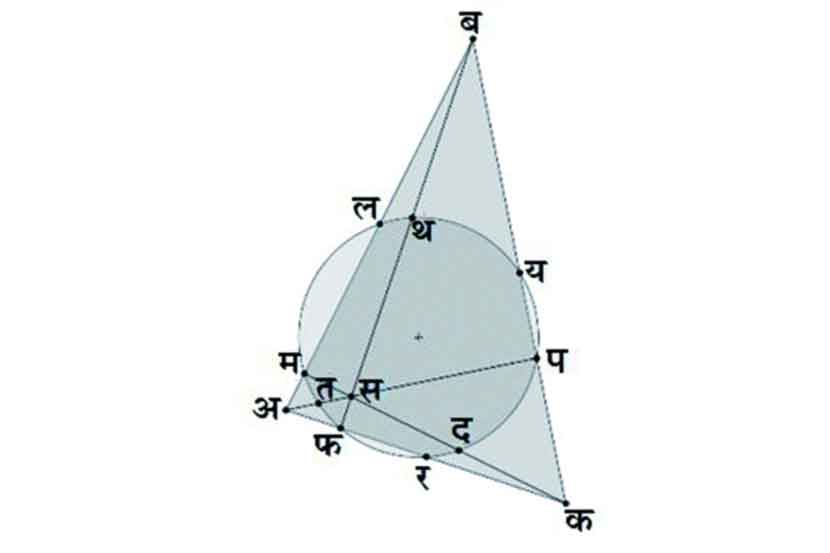
नऊ या अंकाशी निगडित अनेक वैशिष्टय़पूर्ण संकल्पना आहेत, उदा. साहित्यातील नवरस, नवरात्र, अकबराच्या दरबारातील नवरत्ने; तसेच भूमितीतील नवबिंदू वर्तुळ! त्रिकोणाच्या संदर्भात नऊ विशेष बिंदूंतून जाणारे हे वर्तुळ ऑयलरचे वर्तुळ किंवा फेरबाख (Feurabh)) वर्तुळ म्हणूनही प्रसिद्ध आहे. ते नऊ बिंदू म्हणजे- आकृतीत दर्शवलेल्या एका त्रिकोणाच्या तीन बाजूंचे मध्यबिंदू (य, र, ल), तीन लंबपादबिंदू (प, फ, म) (फीट ऑफ अल्टिटय़ूड्स), त्रिकोणाचा प्रत्येक शिरोबिंदू आणि लंबसंपात स (ऑर्थोसेंटर) या दोन बिंदूंना जोडणाऱ्या अस, बस, कस या तीन रेषाखंडांचे मध्यबिंदू (त, थ, द). लिओनार्ड ऑयलर यांनी १७६५ मध्ये त्रिकोणाचे लंबसंपात, मध्यगासंपात (सेंट्रॉइड) आणि परिकेंद्र (सर्कमसेंटर) हे बिंदू एकरेषीय असतात हे सिद्ध केले; (ऑयलर रेषा). नवबिंदू वर्तुळाचा केंद्रबिंदूही याच रेषेवर असतो.
नवबिंदू वर्तुळाचे काही गुणधर्म :
१) समभुज त्रिकोणात नवबिंदू वर्तुळाचा केंद्रबिंदू आणि परिकेंद्र हे एकच असतात.
२) त्रिकोणाचा लंबसंपात आणि त्रिकोणाच्या परिवर्तुळावरील कोणताही बिंदू जोडून येणारा रेषाखंड नवबिंदू वर्तुळ दुभागते.
३) नवबिंदू वर्तुळाची त्रिज्या त्रिकोणाच्या परिवर्तुळाच्या त्रिज्येच्या निम्मी असते. म्हणून नवबिंदू वर्तुळाचे क्षेत्रफळ त्या त्रिकोणाच्या परिवर्तुळाच्या क्षेत्रफळाच्या १/४ पट असते. आणि
४) समजा, त्रिकोणाचा लंबसंपात ‘‘स’’, मध्यगासंपात ‘‘ग’’, परिकेंद्र ‘‘ह’’, नवबिंदू वर्तुळाचा केंद्रबिंदू ‘‘न’’ असेल तर हन = नस आणि नस = ३ नग.
नवबिंदू वर्तुळाच्या अशा वैशिष्टय़पूर्ण गुणधर्मावर आधारित प्रश्नांचा अभ्यास गणित ऑलिम्पियाडसारख्या परीक्षांसाठी करावा लागतो.
कार्ल विल्हेम फेरबाख या गणितीने १८८२ मध्ये नवबिंदू वर्तुळ त्रिकोणाच्या आंतरवर्तुळाला आतून, तर तीन बावर्तुळांना (एक्स-सर्कल) बाहेरून स्पर्श करते, हे सिद्ध केले. त्रिकोणाच्या बाभागात असलेले, त्रिकोणाच्या एका बाजूला स्पर्श करणारे व इतर दोन बाजू वाढवून त्यांनाही स्पर्श करणारे वर्तुळ म्हणजे त्रिकोणाचे बावर्तुळ. १८९२ मध्ये मॅक्झिम बुचर या अमेरिकन गणितज्ञाने त्रिकोणाचे तीन शिरोबिंदू आणि त्याच प्रतलातील आणखी एक बिंदू घेऊन नवबिंदू विवृत्त (एलिप्स) व नवबिंदू अपास्त (हायपरबोला) काढता येतात हे दाखवले.
असे हे अचंबित करणारे नवबिंदू वर्तुळ! एक छोटीशी कृती करा : कोणताही एक त्रिकोण घेऊन त्याचे नवबिंदू वर्तुळ काढा. तसेच त्या त्रिकोणाच्या तीन बाजूंचे मध्यबिंदू जोडून जो त्रिकोण मिळेल, त्याचे परिवर्तुळ काढा. या दोन्ही वर्तुळांचा केंद्रबिंदू एकच आहे असे दिसेल. हे सिद्ध करता येईल का, पाहा बरे!
– शोभना नेने
मराठी विज्ञान परिषद
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org