तर्कशुद्ध पद्धतीने सिद्ध केलेली प्रमेये हा गणिताचा मूलाधार! प्रतल भूमितीत महत्त्वपूर्ण भर घालणारी काही प्रमेये अलेक्झांड्रियाचे पापूस यांच्या नावावर आहेत. त्यांचा आयुष्यकाळ अंदाजे इ.स. २९० ते ३५० असा मानला जातो. ही प्रमेये त्यांनी इ.स. ३४० साली लिहिलेल्या सिनागॉग (Synagoge) म्हणजे त्यांच्या समग्र कामाचे संकलन केलेल्या ग्रंथात दिली होती. त्यातील दोन प्रमेये महत्त्वाची आहेत. तांत्रिकदृष्टय़ा एकाला ‘पापूसचे षटकोन’ प्रमेय आणि दुसऱ्याला ‘पापूसचे मध्यगासंपात किंवा प्रकेंद्र (सेंट्रॉइड)’ प्रमेय अशी नावे आहेत. आपण इथे केवळ पहिल्या प्रमेयाची चर्चा करू.
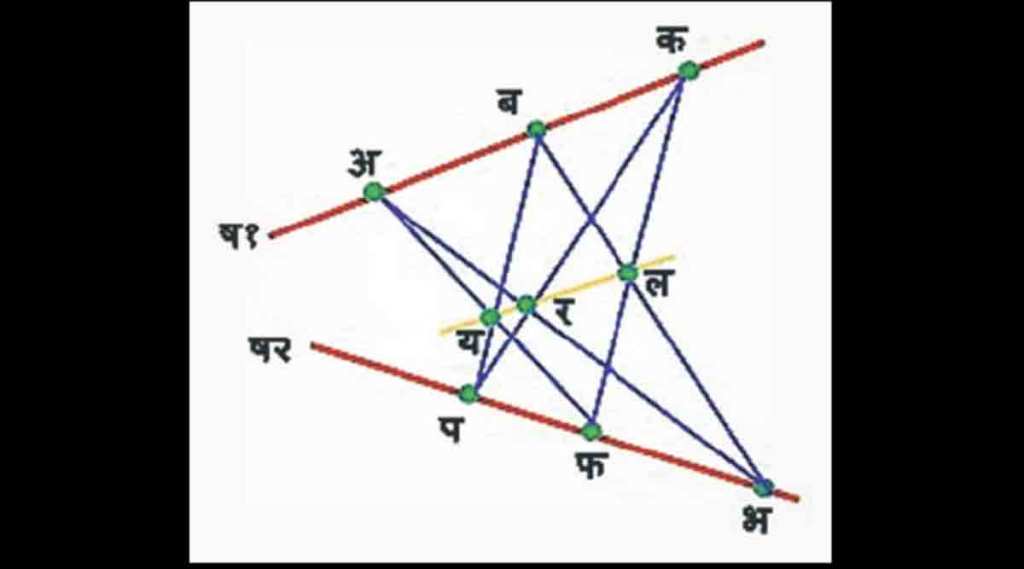
सोबतची आकृती आपण या प्रमेयाचा विचार करण्यासाठी वापरू. त्याप्रमाणे ष१ ही एक रेषा घेऊ आणि तिच्यावर कुठेही यादृच्छिक (रॅण्डम) पद्धतीने अ, ब आणि क हे बिंदू घेऊ, तसेच ष२ ही स्वतंत्र रेषा घेऊन तिच्यावर यादृच्छिक पद्धतीने प, फ आणि भ हे बिंदू घेऊ. नंतर ष१ वरील अ बिंदूला ष२ वरील फ आणि भ बिंदूंना; ब बिंदूला प आणि भ; आणि क बिंदूला प आणि फ बिंदूंना सरळ रेषेने जोडले तर या रेषांचे य, र आणि ल असे छेदनबिंदू मिळतात. पापूसचे प्रमेय सांगते की अशा प्रकारे निर्माण झालेले य, र आणि ल बिंदू नेहमी एक रेषेवर असतील. या प्रमेयाचे वैशिष्टय़ असे की कुठलेही मोजमाप न करता केवळ बिंदू आणि रेषा यांच्या आपाताने (इन्सिडन्सने) कुठल्याही परिस्थितीत एका नव्या सरळ रेषेची निर्मिती होते. तरी त्यांच्या सन्मानार्थ, य, र आणि ल बिंदूंना जोडणारी रेषा ‘पापूसची रेषा’ या नावाने संबोधली जाते. सदर प्रमेयाची सिद्धता विविध पद्धतींनी देता येते.
लाक्षणिक अर्थाने पापूसनंतर काही शतकांनी विकसित झालेल्या प्रक्षेप (प्रोजेक्टिव्ह) भूमितीची बीजे या प्रमेयामुळे रोवली गेली. भूमिती आणि बीजगणित यांनादेखील हे प्रमेय जोडत असल्याने त्याचे अनन्यसाधारण महत्त्व आहे. पापूसचे प्रमेय प्रत्यक्ष नियोजनात वापरलेही जाऊ शकते. उदाहरणार्थ, समजा संत्र्याची नऊ झाडे दहा रेषांत अशी लावायची आहेत की प्रत्येक रेषेवर तीन झाडे असली पाहिजेत. आपण आकृतीत तीन बिंदू असलेल्या ष१, ष२, अफ, अभ, बप, बभ, कप, कफ आणि यल अशा नऊ रेषा मिळवल्या आहेत, तरी ब बिंदू थोडा हलवून ‘बरफ’ अशी दहावी रेषा मिळवली जाऊ शकते. या प्रमेयाचे व्यापकीकरण (जनरलायझेशन) अनेक दिशांनी झाले आहे. त्याची सुरुवात १६ सोळाव्या शतकात ब्लेझ पास्कल या फ्रेंच गणितीने १६४० मध्ये केली होती, तरीही अधिक संशोधनास वाव आहे.
– डॉ. विवेक पाटकर
मराठी विज्ञान परिषद, वि. ना. पुरव मार्ग, चुनाभट्टी, मुंबई २२ office@mavipamumbai.org