समजा अ = {२, ३, ५, ७} आणि ब = {१, २, ४, ५, ६} असे दोन संच आहेत. व्याख्येप्रमाणे त्या दोघांचा संयोग (युनियन) असा संच निर्माण करेल, ज्यात अ किंवा ब संचातील घटक असतील आणि सारखे असलेले घटक एकदाच घेतले जातील. म्हणजे अ ∪ ब = {१, २, ३, ४, ५, ६, ७}. त्याशिवाय त्या संचांचा छेदसंच (इंटरसेक्शन सेट) सुद्धा निर्माण करता येईल, ज्यात दोन्ही संचांतील केवळ सारखे असलेलेच घटक असतील, म्हणजे ∩ ब = {२, ५}. नोंद करण्याची बाब म्हणजे अ संचात चार घटक आहेत म्हणजे |अे = ४, तसेचेबे= ५,|अ ∪ बे = ७ आणिे∩ बे = २. यावरून लक्षात येते की|अ ∪ बे =|अे +|बे-|∩ बे. म्हणजे दोन संचांच्या संयोगाचे प्रगणन करताना मूळ संचांचा समावेश करणे आणि त्यातून छेदसंचाला बाद करणे असे आहे.
याला औपचारिक भाषेत ‘समावेशन-अपवर्जन तत्त्व’ किंवा घेणे-वगळणे तत्त्व (इंक्लूझन-एक्सक्लूझन प्रिन्सिपल) म्हटले जाते. संगणकशास्त्र, चयनशास्त्र (कॉम्बिनेटोरिक्स), संभाव्यता सिद्धांत इत्यादी क्षेत्रांत या तत्त्वाचा लक्षणीय उपयोग होतो.
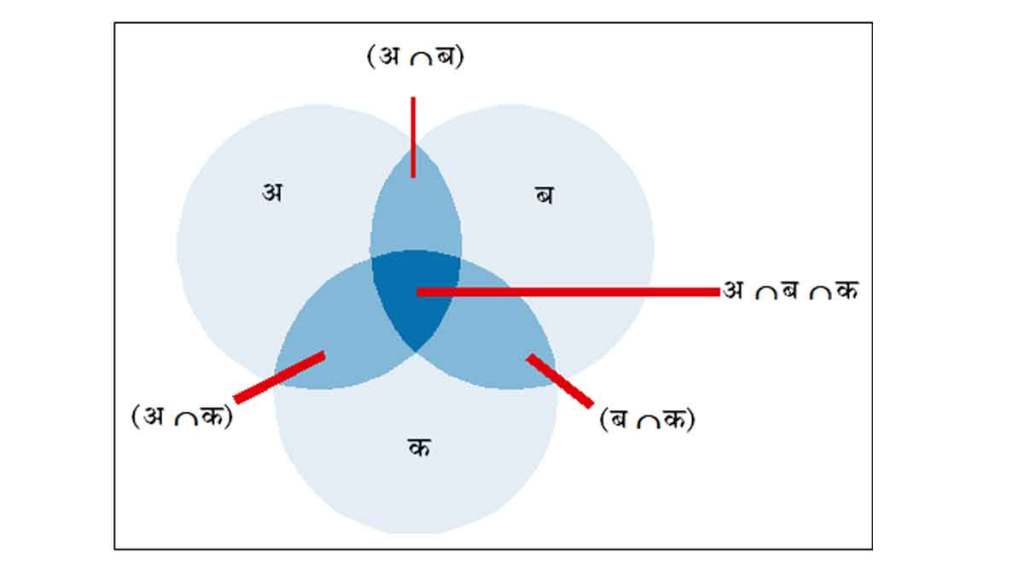
दोनहून अधिक सान्त संख्यांचे संच असल्यास या सूत्राचे व्यापक स्वरूप वापरता येते. तीन संचांच्या बाबतीत आकृती बघावी. समावेशन-अपवर्जन तत्त्वाच्या तार्किक चौकटीप्रमाणे |अ ∪ ब ∪ के =|अे +|बे +|के -|∩ बे -|∩ के-|बू के +|अ ∪ ब ∪ के. उदाहरणार्थ, एका वर्गातील ५४ विद्यार्थ्यांना केवळ क्रिकेटमध्ये (अ), ३७ विद्यार्थ्यांना केवळ फुटबॉलमध्ये (ब) आणि २३ विद्यार्थ्यांना केवळ हॉकीमध्ये (क) रस आहे. त्याशिवाय २१ विद्यार्थ्यांना क्रिकेट आणि फुटबॉलमध्ये (अ ∪ ब), १५ विद्यार्थ्यांना क्रिकेट आणि हॉकीमध्ये (अ ∪ क), १० विद्यार्थ्यांना फुटबॉल आणि हॉकीमध्ये (ब ∪ क) आणि ७४ विद्यार्थ्यांना यापैकी कुठल्या तरी एका खेळात (अ ∪ ब ∪ क) रस आहे. तर वर्गात तिन्ही खेळांत रस असणारे किती विद्यार्थी आहेत? वरील सूत्रानुसार, ७४ = ५४ + ३७ + २३ – २१ – १५ – १० +|अ ∪ ब ∪के प्राप्त होते. त्यावरूनेअ ∪ ब ∪ के = ६, म्हणजे सहा विद्यार्थ्यांना तिन्ही खेळांत रस आहे हे समजते.
या तत्त्वाचे एक पर्यायी रूप अंकशास्त्रात महत्त्वाचे योगदान देते. त्याशिवाय मनुष्यबळ, यं{ आणि कार्य यांचे सर्वोत्तम वितरण व्हावे अशा व्यवस्थापनात समावेशन-अपवर्जन तत्त्व कळीची भूमिका बजावते.
– डॉ. विवेक पाटकर मराठी विज्ञान परिषद,
संकेतस्थळ : http://www.mavipa.org
ईमेल : office@mavipamumbai.org