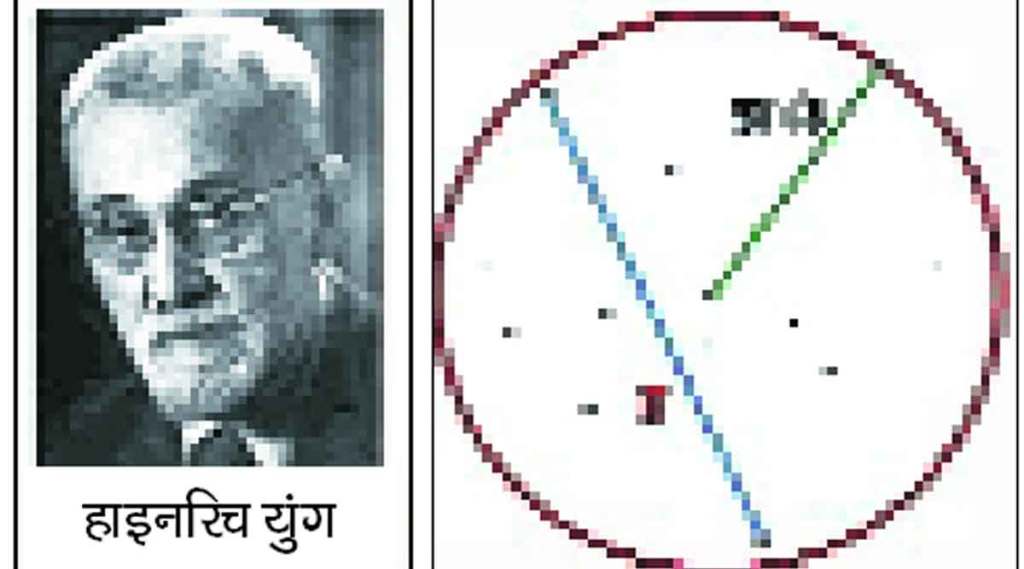
प्रतल भूमितीत एक नवे प्रमेय १९०१ साली जर्मन गणितज्ञ हाइनरिच युंग (१८७६-१९५३) यांच्या योगदानाने जोडले गेले. ते असे : समजा प्रतलावर काही बिंदू विखुरलेले आहेत, जसे की एखाद्या नकाशावर किंवा कागदावर यादृच्छिक (रॅण्डम) पद्धतीने पडलेले तेलाचे वा रंगाचे ठिपके. त्यातील दोन एकमेकांपासून सर्वात दूर असे बिंदू निवडायचे, जे निरीक्षणाने किंवा पट्टीने मोजून ठरवता येतील. समजा ते कमाल अंतर ‘ड’ आहे. त्या ‘ड’ अंतराला भौमितिक विस्तार (स्पॅन) म्हणतात. तर युंगचे प्रमेय सांगते की बिंदू कसेही विखुरलेले असोत, त्या सर्व बिंदूंना निश्चितपणे सामावून घेणारे एक वर्तुळ काढता येईल, ज्याची त्रिज्या (ड/न्न्३) पेक्षा मोठी नसेल.
या प्रमेयाची एक विशिष्ट बाब म्हणून समजा प्रतलावर तीन बिंदू घेतले, जे जोडून समभुज त्रिकोण बनतो आणि त्याची प्रत्येक भुजा एक एकक आहे म्हणजे ड = १. त्या स्थितीत, त्या तिन्ही बिंदूंना सामावून घेणारे असे वर्तुळ त्या समभुज त्रिकोणाच्या शिरोबिंदूंतून जाईल आणि त्याची त्रिज्या १/न्न्३ असेल. प्रमेयाची युंग यांनी दिलेली मूळ सिद्धता आणि नंतर १९०९ साली दिलेली दुसरी सिद्धताही बरीच क्लिष्ट होती. मात्र त्याची सुटसुटीत सिद्धता एल. एम. ब्लुमेंथल आणि जी. ई. वॅहलीन यांनी १९४१ साली दिली.
या प्रमेयाचे व्यापकीकरण (जनरलायझेशन) उच्च मितीमध्ये केले गेले आहे जसे की त्रिमितीमध्ये. त्यानुसार वरील व्याख्या मानून असे बिंदू एका गोलात (स्फिअर) सामावून जातील, ज्याची त्रिज्या (न्न्६ड/४) पेक्षा मोठी नसेल. त्या पुढे जाऊन ‘न’ मितीमध्ये अशा अतिगोलाची (हायपरस्फिअर) त्रिज्या ड[न्न्(न/(२5(न+१)] पेक्षा मोठी नसेल. उदाहरणार्थ, चतुर्मिती म्हणजे न=४ असल्यास, त्या अतिगोलाची त्रिज्या [ड(न्न्(२/५)] पेक्षा मोठी नसेल.
इतकेच नव्हे तर युंगचे प्रमेय युक्लीडेतर (नॉन-युक्लीडियन) भूमितीसाठी व अवकाशांसाठीही सिद्ध केले गेले आहे.
गणिताच्या अन्य शाखांशिवाय या प्रमेयाचे उपयोजन विविध क्षेत्रांत शक्य आहे, जसे की समुद्रात हरवलेल्या नौकेचा शोध घेणे, पोलिसांचे गस्त घालण्याचे क्षेत्र आखणे, दुकानात किंवा कोठारात माल इष्टतमरीत्या रचून ठेवणे इत्यादी. कर्करोगासाठी रुग्णाला दिल्या जाणाऱ्या विकिरण (रेडिएशन) उपचार पद्धतीत युंगच्या प्रमेयाचा उपयोग करून कमाल फायदा मिळू शकतो असे २०१८ साली एका शोधलेखात दाखवले गेले आहे. त्यात विकिरण देणाऱ्या उपकरणाचा प्रकाशझोत (बीम) शरीरावर आखलेल्या किंवा अपेक्षित क्षेत्रात पडेल हे निश्चित करण्यासाठी आणि तसे घडले आहे, याचा मागोवा घेण्यासाठी युंगच्या प्रमेयावर आधारित गणनप्रक्रिया कळीची भूमिका बजावते. आहे ना प्रमेय बहुमोल!
– डॉ. विवेक पाटकर मराठी विज्ञान परिषद,
वि. ना. पुरव मार्ग, चुनाभट्टी, मुंबई २२
office@mavipamumbai.org